已知椭圆 \(C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}(a>b>0)\) 的左右焦点分别为为 \(F_1,F_2,\)
过 \(F_1\) 的直线 \(l\) 交 \(C\) 于 \(A,B\) 两点. 若 \(\overrightarrow{AF_1}=\dfrac{4}{7}\overrightarrow{AB}, |AF_2|=|F_1F_2|,\) 则椭圆 \(C\) 的离心率为 \((\qquad)\)
\(\mathrm{A.}\dfrac{2}{7}\qquad\) \(\mathrm{B.} \dfrac{3}{7}\qquad\) \(\mathrm{C.}\dfrac{4}{7}\) \(\mathrm{D.}\dfrac{5}{7}\)

解析: 法一 如图

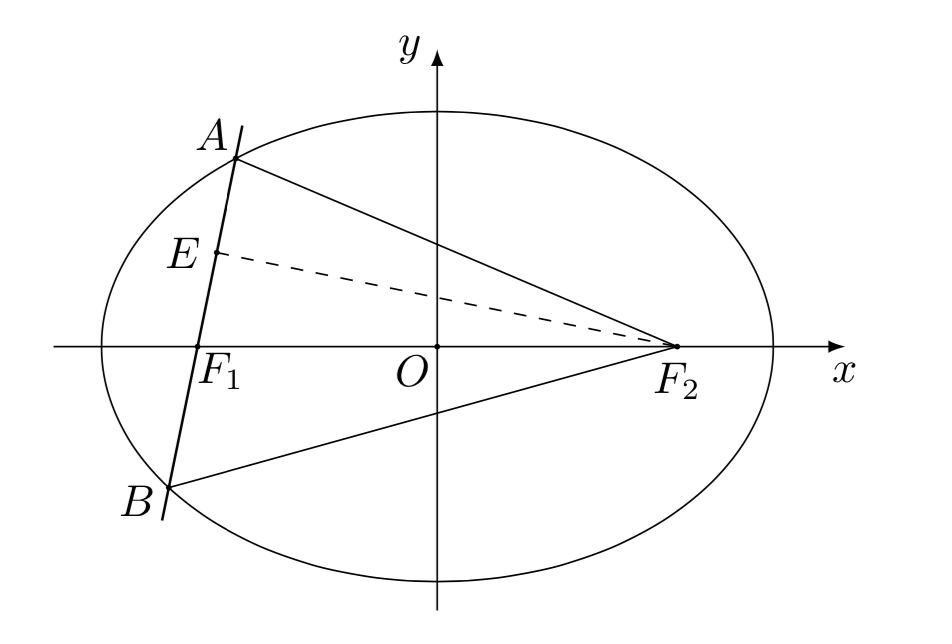
根据题意知 \(|AF_2|=2c,\) 结合椭圆的定义得
\[ |AF_1|=2(a-c),\]
又 \(\overrightarrow{AF_1}=\dfrac{4}{7}\overrightarrow{AB}\), 则 \[|BF_1|=\dfrac{3}{2}(a-c), |BF_2|=\dfrac{1}{2}(a+3c) .\]
取 \(AF_1\) 的中点 \(E,\) 连接 \(F_2E,\)
又因为 \[ |AF_2|=|F_1F_2| ,\]所以在 $ \mathrm{Rt} \triangle EF_2A,\mathrm{Rt} \triangle EF_2B$ 中, 应用勾股定理得
\[AE^2+EF_2^2=AF_2^2,BE^2+EF_2^2=BF_2^2,\]
代入数值并运算可得 \(7c=5a\text{ 或 } a=c\) $( $舍去 \(),\)
所以 \(e=\dfrac{5}{7},\) 选项 \(\mathrm{D}\) 正确.

法二 设椭圆的半焦距 为 $ c$.

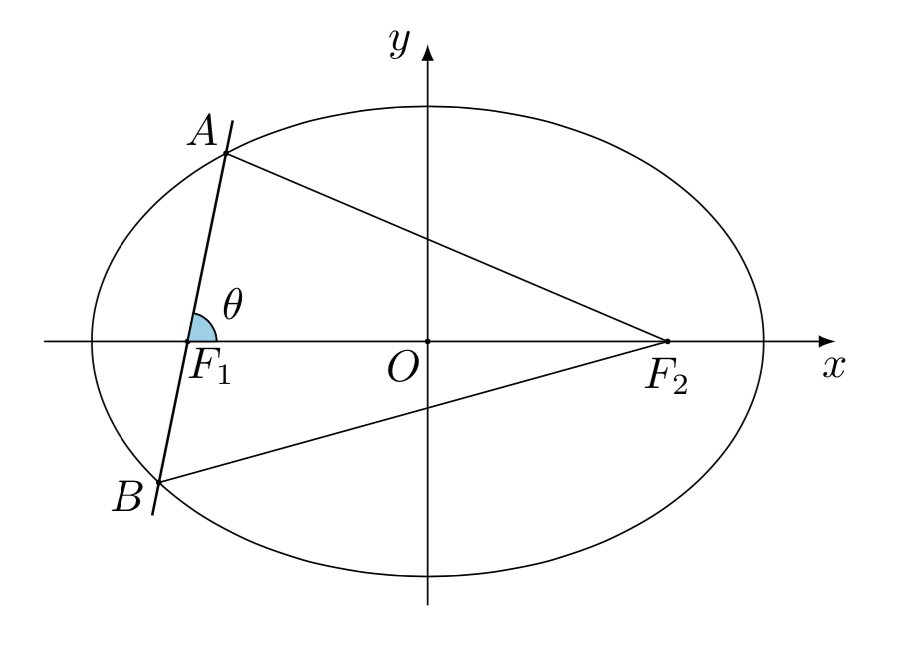
如图, 设 \(\angle AF_1F_2=\theta\), 则由椭圆的焦半径公式 \(\mathrm{II}\) 可得
\[ |AF_1|=\dfrac{ep}{1-e\cos\theta}, |BF1|=\dfrac{ep}{1+e\cos\theta}, \]
其中 \(p\) 为椭圆的焦准距, \(p=\dfrac{b^2}{c}\). 由 \(\overrightarrow{AF_1}=\dfrac{4}{7}\overrightarrow{AB}\) 可得
\[ \dfrac 43=\dfrac{|AF_1|}{BF_1}=\dfrac{1+e\cos\theta}{1-e\cos\theta}. \]
解得 \(e\cos\theta =\dfrac 17\). 从而可得
\[ 2c=|F_1F_2|=|AF_2|=2a-|AF_1|=2a-\dfrac{ep}{1-\frac 17}=2a-\dfrac 76\cdot \dfrac{b^2}{a}. \]
将 \(b^2=a^2-c^2\) 代入并整理可得 \((5a-7c)(a-c)=0\), 因此所求离心率为 \(\dfrac57\).