声明来自各大网站以及博文资料整合,仅供学习使用
帕斯卡分布
帕斯卡分布,负二项分布的正整数形式,描述第n次成功发生在第x次的概率,是统计学上一种离散概率分布。
在重复、独立的伯努利试验,设每次试验成功的概率为p,失败的概率为q= 1- p,若将试验进行到出现r(r为常数)次成功为止,以随机变量X表示所需试验次数,则 X是离散型随机变量,其概率分布为:P(x = k) = C(r-1,k-1)q(r-1)*p,k = r ,r + 1…
,此时称P(x = k)服从帕斯卡分布。其中p表示每次试验出现成功的概率,而q=1-p,它的期望为r/p,方差为rq/p2,当r=1时,即为几何分布帕斯卡(Pas-cal , B.)。
举例
举例说,若我们掷骰子,掷到一即视为成功。则每次掷骰的成功率是1/6。要掷出三次一,所需的掷骰次数属于集合{ 3, 4, 5, 6, … }。掷到三次一的掷骰次数是负二项分布的随机变数。要在第三次掷骰时,掷到第三次一,则之前两次都要掷到一,其概率为(1/6)3。注意掷骰是伯努利试验,之前的结果不影响随后的结果。
应用(来源百度百科)


二项分布
(来源于百度知道)
二项分布就是重复n次独立的在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。二项分布就是重复n次独立的伯努利试验。
伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型。
当试验次数为1时,二项分布服从0-1分布。

单个伯努利试验是没有多大意义的,然而,当我们反复进行伯努利试验,去观察这些试验有多少是成功的,多少是失败的,事情就变得有意义了,这些累计记录包含了很多潜在的非常有用的信息。
若某事件概率为p,现重复试验n次,该事件发生k次的概率为:P=C(k,n)×pk×(1-p)(n-k).C(k,n)表示组合数,即从n个事物中拿出k个的方法数.
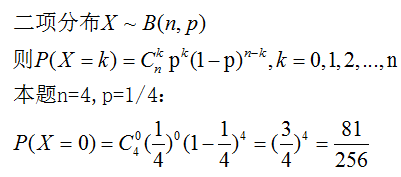
注意:
- n次试验在相同条件下进行,且各个观察单位的观察结果相互独立,即每个观察单位的观察结果不会影响到其他观察单位的结果。如要求疾病无传染性、无家族性等 。
- 各观察单位只能具有相互对立的一种结果,如阳性或阴性,生存或死亡等,属于两分类资料。
应用实例

在计算中常用泊松定理(来源DrCrypto csdn)

超几何分布 V.S. 二项分布:
(来源于百灵雀的博客)
两者都是抽样,只不过超几何分布是无放回抽样,二项分布是有放回抽样。当超几何分布中N很大,而n很小时,无放回抽样可以近似得看成有放回抽样,也就是超几何分布可以用二项分布近似。
泊松分布
在n重伯努利试验中,事件A在每次试验中发生的概率为p,出现A的总次数K服从二项分布b(n,p),当n很大p很小,λ=np大小适中时,二项分布可用参数为λ=np的泊松分布来近似。
把时间切成很小的片,那么每个时间片里发生的事件是相互独立的,便可以用二项分布的思想来解。另一方面看,使用泊松定理可以近似计算二项分布。λλ是固定时间间隔内平均发生事件的次数
把连续的时间分割层无数小份,那么每个小份之间都是相互独立的。在每个很小的时间区间内,事情可能发生也可能不发生,因此这就是一个p很小的二项分布。连续的时间分成无数小份,也就意味着n很大,即:泊松分布是二项分布的一种极限形式。
特性百度百科
考虑下列现象:每小时服务台访客的人数,每天家中电话的通数,一本书中每页的错字数,某条道路上每月发生车祸的次数,生产线上的疵品数,学生到办公室找老师的次数……。大致上都有一些共同的特征:在某时间区段内,平均会发生若干次「事件」,但是有时候很少,有时又异常地多,因此事件发生的次数是一个随机变数,它所对应的机率函数称为 Poisson 分配。

实列1
(摘录于weixin_30239339的博客)
它们的特点就是,我们可以预估这些事件的总数,但是没法知道具体的发生时间。已知平均每小时出生3个婴儿,请问下一个小时,会出生几个?
有可能一下子出生6个,也有可能一个都不出生。这是我们没法知道的。
泊松分布就是描述某段时间内,事件具体的发生概率。
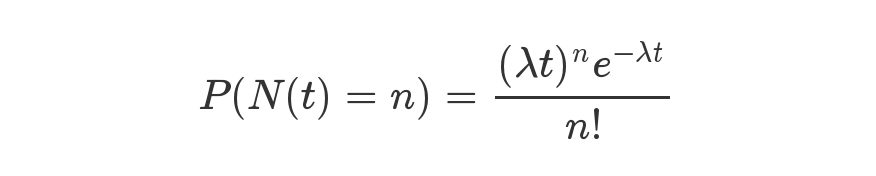
上面就是泊松分布的公式。等号的左边,P 表示概率,N表示某种函数关系,t 表示时间,n 表示数量,1小时内出生3个婴儿的概率,就表示为 P(N(1) = 3) 。等号的右边,λ 表示事件的频率。
接下来两个小时,一个婴儿都不出生的概率是0.25%,基本不可能发生。
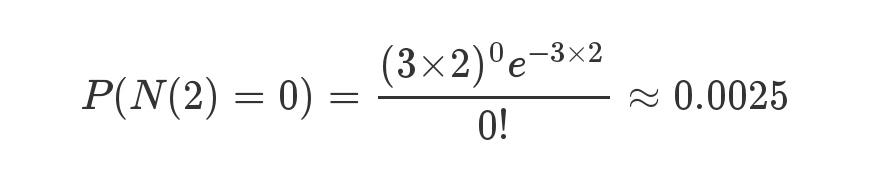
接下来一个小时,至少出生两个婴儿的概率是80%。

大概分布图
实例2(摘录于DrCrypto )
指数分布

泊松分布 V.S. 二项分布:
(来源于百灵雀的博客)

指数分布
(来源于百度百科)
指数函数的一个重要特征是无记忆性(Memoryless Property,又称遗失记忆性)。这表示如果一个随机变量呈指数分布,当s,t>0时有P(T>t+s|T>t)=P(T>s)。即,如果T是某一元件的寿命,已知元件使用了t小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等。
概率密度函数
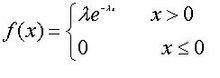
指数分布的分布函数
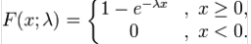 特性
特性


示例
(来源于seo实验室小编)


示例2
(来源于百度文库Silence)


正态分布
来源于百度百科
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

正态分布的特性


正态分布表


示例


均匀分布



引用:
- 帕斯卡分布的应用来源百度百科
- 二项分布部分来源于百度知道
- 在计算中常用泊松定理**来源DrCrypto csdn
- 超几何分布 V.S. 二项分布来源于百灵雀的博客
- 泊松分布特性来源于百度百科
- 泊松分布实例1摘录于weixin_30239339的博客
- 泊松分布实例2摘录于DrCrypto
- 泊松分布 V.S. 二项分布来源于百灵雀的博客
- 指数分布来源于百度百科
- 指数分布示例来源于seo实验室小编
- 指数分布示例2来源于百度文库Silence
- 正态分布来源于百度百科
- 部分题目来源于百度文库
