写在前面

如果读者已经熟练理解、掌握了算法渐近分析方法，那么以下内容将不会对读者有任何的价值，如果十分珍惜自己的时间请务必跳过。

说明

1. 文中 alg 都表示算法（algorithms）;
2. 文中 n 都表示问题规模；

渐近分析的基本思想

1. 忽略掉依赖于机器的常量；
2. 不去检查alg的实际运行时间，而是关注随着问题规模的增长，运行时间的增长率；

增长率展示了规律，问题规模n，与alg运行时间T(n)的函数关系。如果取多次运行时间的平均值来进行比较并不能说明问题，统计的思想在算法分析方面并不是十分适用。

渐近符号

1. O（big-oh） :  称为 上界 （上限界限）
2. Ω （big-omege）:  称为 下界 （下限界限）
3. Θ （big-theta） : 称为 精确界
4. o (little-oh) ： 称为 非渐近紧确上界
5. ω (little-omege) : 称为 非渐近紧确下界

渐近符号数学定义

• O （big-oh）定义 ： 设f(n) 和 g(n) 是定义域为自然数集上的函数。如果存在 c , n0 (c ≥ 0 , n0 ≥ 0 )  , 使得对于一切的 n ≥ n0 都有 0 ≤ f(n) ≤ g(n) 成立 ， 则称 f(n) 渐近的上界是 g(n) , 记作 f(n) = O(g(n)) 。在 n ≥ n0 成立时，函数 f(n) 的阶不会高于函数 g(n) 的阶。

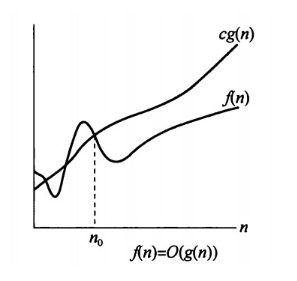
 当  n 在 0 <= n <= n0 这个范围内时， f(n)  是不一定会小于 g(n) 的 ， 但是当 n > n0 后，f(n) 将永远不会再超越 g(n)  。

• Θ （big-theta）定义 ：  设f(n) 和 g(n) 是定义域为自然数集上的函数。如果 lim(n -> ∞) f(n) / g(n) 存在 ， 并且等于某个常数 c (c > 0) , 那么 f(n) = Θ(g(n)) .  

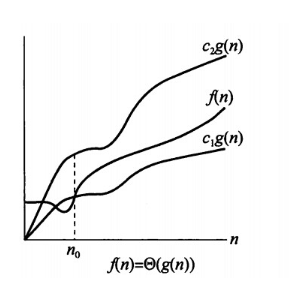
    存在大于 0 的常量 c1 , c2 , n0 , 使得对于所有的 n > n0 , 都有 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) 。 f(n) 属于集合 Θ(g(n)) 。

• Ω （big-omege） ：　设f(n) 和 g(n) 是定义域为自然数集上的函数。如果存在 c , n0 (c ≥ 0 , n0 ≥ 0 )  , 使得一切　ｎ ≥ ｎ０　都有　0 ≤ g(n) ≤ f(n)　成立，则称　f(n) 的渐近下界是 g(n) , 记作 f(n) = Ω(g(n)) 

扫描二维码关注公众号，回复： 82828 查看本文章

• o (little-oh)  :  设 f(n) 和 g(n) 是定义域为自然数集N上的函数。若对于任意正数 c 都存在n0，使得对一切  n ≥ n0 都有 0 ≤ f(n) < cg(n) 成立，则称 f(n) 的渐进的非紧确上界是 g(n)，记作f(n)=o(g(n)) 。通俗的说n满足一定条件范围内，函数f(n) 的阶低于函数g(n) 。

• ω (little-omege) ： 设 f(n) 和 g(n) 是定义域为自然数集N上的函数。若对于任意正数 c 都存在n0，使得对一切  n ≥ n0 都有 0 ≤ cg(n) < f(n) 成立，则称 f(n) 的渐进的非紧确下界是 g(n)，记作f(n)=ω(g(n)) 。通俗的说n满足一定条件范围内，函数f(n) 的阶高于函数g(n) 。