矩乘入门学习笔记

<前言>

前几天和hxc神仙说想入门一下矩乘。

神仙甩手给我三道题说这几道题会写了那就入门了。

分别是luoguP3702、luoguP5303、CF1182E.

稍微看了一下luogu评分，两黑一紫。。

稍微写了一道P5303就不会。最后终于是在看题解的情况下找到了我对矩乘理解上的错误。。。怪不得一直调不出来。

正文

P5303[GXOI/GZOI2019]逼死强迫症

大佬们一看题目就知道是斐波那契的变式。

我看了好久也没看出来。

50%

这题不用矩乘加速的话，就是个递推。

设\(f_i\)表示\(2 \times i\)的方格满足条件的方案数。

如何从已有状态转移？

我们先考虑从i-1转移到i状态。新加入一列\(1 \times 2\)的空地

可以直接放入一块竖的砖，方案数就是加上\(f_{i-1}\)的值，因为不改变\(1 \times 1\)的方格的取值。
我们再考虑从i-2转移。

你也可以在这么空出的\(4\times 4\)的格子中放入两个横的\(1 \times 2\)的砖，依旧不会改变\(1\times 1\)的方格，方案数加上\(f_{i-2}\)。

你会发现上面的方案都没有包括\(1\times 1\)的方格在新加入列的情况，其他情况都已囊括。

目前转移为
\[ f_i=f_{i-1}+f_{i-2}+x \]
其中x为我们接下来要讨论的值。

设\(g_i\)表示\(2\times i\)只用\(1\times2\)方格填充的方案数。

此时转移就只包括没有包括\(1\times 1\)的方格在新加入列的情况，也就是上面的讨论。

并且初值是\(g_0=1,g_1=1\)，发现这就是个斐波那契数列。特别的，\(g_0=1\)。
那么\(1\times1\)方格在新加入列的情况就是\(2g_{i-1}\)，为什么呢？

如图，黄色部分为斐波那契数列的g方案数，在两边塞入正方形。就变成了这样：

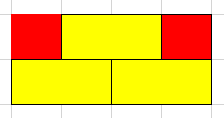
此时只有一种合法方案。但是左边就变成了任意摆放的g。即：

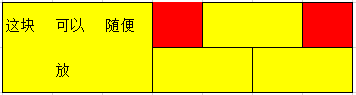
可以证明左边的方格只能放在\(1\) ∼ \(i-2\)的列中且每列恰好可以放一个（因为奇偶性质）。
设它在第k列，则左边方案数为\(g_{k-1}\)，而k取1到i-2.注意右边的矩形上下都可以放，乘个2.
所以方案数为：
\[ 2(g_0+g_1+g_2+g_3……g_{i-3}) \]
g为0开始的斐波那契。
即前缀和。由斐波那契前缀和公式可知上式
\[ \begin{aligned} &= 2 \ g_{i-1} -2\\ \end{aligned} \]

故总的转态转移方程为：

\[ f_i=f_{i-1}+f_{i-2}+ 2\ g_{i-1}-2 \]
这样，你可以拿到50point（^ - ^）

100%

然后是矩乘优化递推。

我们发现\(f_i\)与两项f有关，一项g有关（但因为g的递推要两个位），一项常数有关。

于是用\(5 \times 5\)的矩阵加速递推，初始状态为

\[ \begin{bmatrix} 0&0&1&2&2 \end{bmatrix} \quad \]
递推矩阵为

\[ \begin{bmatrix} 0&1&0&0&0\\ 1&1&0&0&0\\ 0&0&0&1&0\\ 0&2&1&1&0\\ 0&-1&0&0&0 \end{bmatrix} \quad \]

这些东西都出来了，就已经可以套板子了。

注意本题有模数，这意味着我们得做出一些改变，即把-1改为mod-1.

\(\mathrm{Code:}\)

#include <bits/stdc++.h>
#define mod    1000000007
#define int    long long
using namespace std;
int n, T;
int read()
{
    int  s = 0, w = 1;
    char c = getchar();
    while ((c < '0' || c > '9') && c != '-')
        c = getchar();
    if (c == '-')
        w = -1, c = getchar();
    while (c <= '9' && c >= '0')
        s = (s << 3) + (s << 1) + c - '0', c = getchar();
    return s * w;
}
int mul(int a, int b)
{
    return 1LL * a * b % mod;
}
int add(int a, int b)
{
    return a + b >= mod ? a + b - mod : a + b;
}
struct martix
{
    int a[5][5];
    inline martix()
    {
        memset(a, 0, sizeof(a));
    }
    inline martix operator *(martix b)
    {
        martix c;
        for (int i = 0; i < 5; ++i)
            for (int j = 0; j < 5; ++j)
                for (int k = 0; k < 5; ++k)
                    c.a[i][j] = add(c.a[i][j], mul(a[i][k], b.a[k][j]));
        return c;
    }
}   f, d;
int fx[5]    = { 0, 0, 1, 2, 2 };
int dx[5][5] =
{
    { 0,       1, 0, 0, 0 },
    { 1,       1, 0, 0, 0 },
    { 0,       0, 0, 1, 0 },
    { 0,       2, 1, 1, 0 },
    { 0, mod - 1, 0, 0, 1 }
};
martix power(martix a, int b)
{
    martix s;
    for (int i = 0; i < 5; ++i)
        s.a[i][i] = 1;
    for (; b; b >>= 1)
    {
        if (b & 1)
            s = s * a;
        a = a * a;
    }
    return s;
}
signed main()
{
    T = read();
    while (T--)
    {
        memcpy(f.a, fx, sizeof(fx));
        memcpy(d.a, dx, sizeof(dx));
        n = read();
        if (n == 0 || n == 1 || n == 2)
        {
            printf("0\n"); continue;
        }
        f = f * power(d, n - 1);
        printf("%lld\n", f.a[0][0]);
    }
    return 0;
}

这题在调的过程中给了我很多启发，纠正了很多我在理解上的错误。

hxc神仙给的题就是不一般啊。。。

感觉和黑题的差距还有有一些的，即使标签是黑的。

暂时咕到这里，先去写题了。