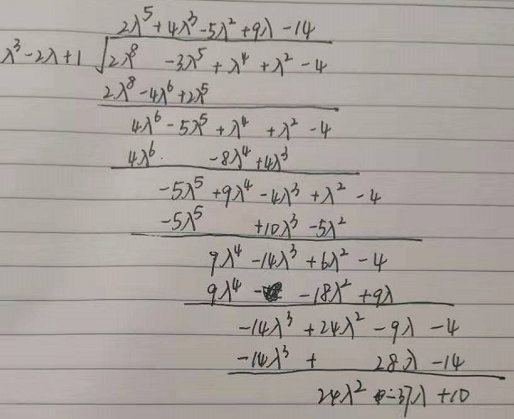我的微信公众号名称:AI研究订阅号
微信公众号ID:MultiAgent1024
公众号介绍:主要研究强化学习、计算机视觉、深度学习、机器学习等相关内容,分享学习过程中的学习笔记和心得!期待您的关注,欢迎一起学习交流进步!
相似变换是矩阵的一种重要的变换,本章研究矩阵在相似变换下的简化问题,这是矩阵理论的基本问题之一。这种分解简介形式在许多领域中都有重要的作用。
在开始之前说一下矩阵的一些基本概念,设矩阵
A=(aij)n×n,将矩阵
A的元素
aij所在的第
i行第
j列划去后,剩余的各元素按原来的排列顺序组成的
n−1阶矩阵所确定的行列式称为元素
aij的余子式,记为
Mij,称
Aij=(−1)i+jMij为元素
aij的代数余子式。
方阵
A=(aij)n×n的各元素的代数余子式
Aij所构成的如下矩阵
A∗:
A11A12⋮A1nA21A22⋮A2n⋯⋯⋯An1x⋮Ann
该矩阵
A∗称为
A的伴随矩阵。具有以下性质:
A∗A=∣A∣E。
哈密顿-凯莱定理以及矩阵的最小多项式
本节讨论特征多项式的性质,并讨论另一种重要的多项式-最小多项式。
哈密顿-凯莱定理
- 定理3.1:(哈密顿-凯莱定理)每个
n阶矩阵都是它的特征多项式的根,设
A为
n阶矩阵,
f(λ)=∣λE−A∣
=λn+an−1λn−1+⋯+a1λ+a0
则
f(A)=An+an−1An−1+⋯+a1A+a0E=O
A=⎝⎛1000−11210⎠⎞
试计算:
φ(A)=2A8−3A5+A4+A2+2E
解 因为多项式为:
f(λ)=∣λE−A∣=λ3−2λ+1
再取多项式:
φ(λ)=2λ8−3λ5+λ4+λ2−4
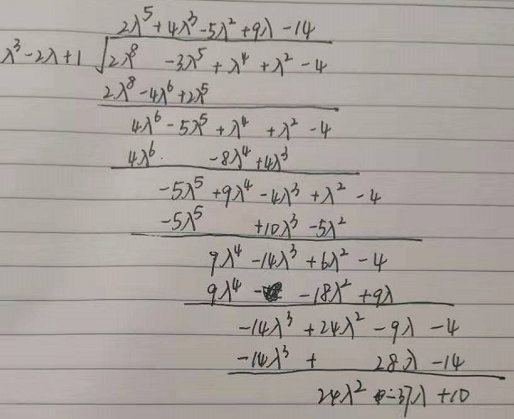
以
f(λ)去除
φ(λ)可得余式:
r(λ)=24λ2−37λ+10
由哈密顿-凯莱定理,
f(A)=O,所以:
φ(A)=r(A)=24A2−37A+10E
=⎝⎛−3004895−61−26−634⎠⎞
最小多项式
一般地说,若
A是一个方阵,
φ(A)是一个多项式,
φ(A)=O,这种多项式叫作矩阵
A的零化多项式,可见每一个矩阵都有零化多项式,并且零化多项式一定有无穷多个,因为特征多项式乘以任何一个多项式还是零化多项式。
那有没有一个次数最低的零化多项式呢?
-
定义3.1:设
A∈Cn×n,在
A的零化多项式中,次数最低的首项系数为1的多项式,称为矩阵
A的最小多项式,记作
m(λ)
-
定理3.2:矩阵
A的任何零化多项式都能被它的最小多项式整除。
-
定理3.3:矩阵
A的最小多项式唯一。
-
定理3.4 :矩阵
A的特征多项式的根一定是最小多项式的根,反过来,最小多项式的根也一定是特征多项式的根。
设矩阵
A∈Cn×n的所有特征值为
λ1,⋯,λs,又
A的特征多项式为:
f(λ)=∣λE−A∣
=(λ−λ1)k1(λ−λ2)k2⋯(λ−λs)ks
则
A的最小多项式一定具有如下形式:
m(λ)=(λ−λ1)n1(λ−λ2)n2⋯(λ−λs)ns
这里
ni≤ki。
矩阵的相似对角
把矩阵化为对角形对于解决很多问题都有帮助,如解微分方程组:
dtdx1=λ1x1dtdx2=λ2x2}
容易解出:
x1=C1eλ1t,x2=C2eλ2t
而
{dtdx1=a11x1+a12x2dtdx2=a21x1+a22x2
如果能化为上一个计算的形式,就很方便求解。
A=⎝⎛00−610−1101−6⎠⎞
是否可以对角化?
解 因为:
f(λ)=∣λE−A∣=(λ+1)(λ+2)(λ+3)
矩阵
A的特征值为-1,-2,-3。
由于
A的三个特征值互不相同,固
A有三个线性无关的特征向量,
A可以对角化,进一步可以得到特征向量:
P1=⎝⎛1−11⎠⎞,P2=⎝⎛1−24⎠⎞,P3=⎝⎛1−39⎠⎞
P=⎝⎛1−111−241−39⎠⎞,
P−1AP=⎝⎛−1−2−3⎠⎞
约当标准形
并不是每个方阵都能够相似于对角矩阵,如果矩阵不能对角化,矩阵总可以通过相似变换化为约当标准形。
Ji=⎝⎜⎜⎛λi1λi⋱1λi⎠⎟⎟⎞ri×ri
的矩阵称为
ri阶约当块,由若干个约当块构成的分块对角矩阵:
J=⎝⎜⎜⎛J1J2⋱Js⎠⎟⎟⎞
称为约当标准形。
- 定理3.6 :设
A∈Cn×n,则
A与一个约当矩阵
J相似,即存在
P∈Cn×n使得
P−1AP=J这个约当矩阵
J除了约当块的排列次序外由矩阵
A唯一确定,称
J为
A的约当标准形。
求解约当标准形
下面我们介绍用行列式因子法确定约当标准形的方法:
设矩阵
A的元素都是
λ的多项式,则
A称为
λ矩阵,记作
A(λ),特殊地,
A∈Cn×n,
λE−A是
A的特征矩阵,这也是
λ矩阵。
公因式:一个多项式中每一项都含有的相同的因式,叫做这个多项式各项的公因式。
- 定义3.3:
A(λ)中所有非零的
k阶子式的首项系数为1的最大公因式
Dk(λ)称为
A的一个
k级行列式因子。
由定义
Dn(λ)=∣λE−A∣,又因为
Dk−1(λ)能够整除每一个
k−1级子式,而每一个
k级子式可以展开为
k−1级子式的线性组合,所以
Dk−1能够整除
Dk,即
Dk−1∣Dk。
d1=D1,d2=D1D2,⋯,dn=Dn−1Dn
称为
A(λ)的不变因子。把每个次数大于零的不变因子分解为互不相同的一次因子的方幂的乘积,所有这些一次因子的方幂(相同的必须按出现次数计算)称为
A的初级因子。
A=⎝⎜⎜⎛−1−212⎠⎟⎟⎞
-
f(λ)=
∣λE−A∣ =
(λ+1)(λ+2)(λ−1)(λ−2)。
行列式因子:
D3=D2=D1=1,D4=f(λ)
不变因子:
d1=d2=d3=1,d4=f(λ)
初级因子:
λ+1,λ+2,λ−1,λ−2
有了上述概念,就可以求得矩阵
A的约当标准形。设
A的全部初级因子是:
(λ−λ1)k1,(λ−λ2)k2,⋯,(λ−λs)ks
这里
λ1,
λ2,
⋯,
λs可能有相同的,指数
k1,
k2,
⋯,
ks也可能有相同的,对每个初级因子
(λ−λi)ki构成一个
ki阶约当块:
Ji=⎝⎜⎜⎛λi1λi⋱⋱1λi⎠⎟⎟⎞(i=1,2,⋯,3)
由所有这些约当块构成的分块对角矩阵:
J=⎝⎜⎜⎛J1J2⋱J1⎠⎟⎟⎞
称为矩阵
A的约当标准形。
- 定理3.7:每个
n阶复数矩阵
A都与一个约当标准形
J相似,即存在矩阵
P使得:
P−1AP=J
除去约当块的排列次序外,约当形矩阵由矩阵
A唯一确定。
史密斯标准形
从上一节可以看到,求出矩阵的行列式因子、不变因子以及初级因子,就可以求出矩阵的约当标准形。而当矩阵阶数比较高时,求它的行列式因子比较麻烦。如果矩阵比较特殊,比方说是对角矩阵,就可以比较方便地求出行列式因子。所以考虑先把矩阵对角化,就可以比较方便地求出行列式因子。所以考虑先把矩阵化为对角形,问题是在把矩阵化为对角形时,矩阵的行列式因子是否改变。
- 定义3.5:下列变换称为矩阵
A的初等变换:
- 互换矩阵
A的任意两行(两列);
- 以非零的数
k乘
A的某一行(列);
- 以多项式
φ(λ)乘以
A的某一行(列)加到另一行(列)上。
可以看出,这三种变换不会改变行列式因子。
A(λ)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛d1(λ)d2(λ)⋱dr(λ)0⋱0⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞
称为矩阵
A的史密斯标准形,其中:
di∣di+1(i=1,2,⋯,r−1)
我们有下面的结论。
- 定理3.8:任何一个非零多项式矩阵
A都可以经过初等变化为史密斯标准形。
下面讨论怎么把一个矩阵
A化为史密斯标准形。假设一个矩阵经过初等变换化为如下形式的标准形:
⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛d1d2⋱drdr+1⋱dn⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞
其中
di∣di+1。
由上面所述,在这个过程中,行列式因子不变,所以变换后的矩阵与原来的矩阵有相同的行列式因子。而这个矩阵的行列式因子很容易得出:
D1=d1,D2=d1d2,⋯,Dn=d1d2⋯dn
由此可以得出,对角线上的元素正好是矩阵的不变因子。
特殊地,左上角的元素为一阶行列式因子,即矩阵的所有元素的公因子。这个公因子可以很容易求出。我们之后就可以利用这个结论求出史密斯标准形。
现在设矩阵
A(λ)是一个
λ矩阵
首先通过观察确定左上角第一个元素,如果矩阵中有这一项,就把它挪到左上角上去,如果没有这一项,可以通过初等变换得出这一项。因为它是所有元素的公因子,能够整除所有元素,也一定能够整除它们的组合,所以可以通过初等变换得到。
左上角的元素得到以后,可以利用初等变换把它所在的行和列的其他元素都消成零,矩阵变成如下形式:
(d100B1(λ))
这时对于矩阵
B1来说,相当于一个新的矩阵,如果把它化成史密斯标准形,则左上角第一个元素仍然是
B1的一阶行列式因子,可以用同样的方法求出,在这个过程中,使用的是初等变换,而
d1能够整除所有元素,当然能够整除它们的组合,所以
d1∣d2,这时矩阵可以通过初等变换化为下面的形式:
⎝⎛d1d1B2(λ)⎠⎞
重复这个过程,即可得到史密斯标准形:
⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛d1d2⋱dr0⋱0⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞