开始之前

各位朋友，大家好！针对上回讲的EM算法，有朋友反馈还是没弄清楚，今天，我再来详细的讲一下EM算法。请耐心食用本教程，滴滴滴~，上车！

前提准备

Jupyter notebook 或 Pycharm
火狐浏览器或谷歌浏览器
win7或win10电脑一台
网盘提取csv数据

需求分析

实现高斯混合模型的 EM 算法(GMM_EM)
高斯混合模型是多个高斯模型的线性叠加而成的，高斯混合模型的概率分布表示如下：

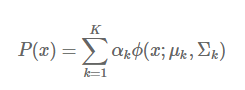
其中，k表示模型的个数， $α_k$ 是第 k 个模型的系数，表示出现该模型的概率，ϕ(x;μk,Σk) 是第 k 个高斯模型的概率分布。

E步：样本 $x_i$来自于第 k 个模型的概率，我们把这个概率称为模型 k 对样本 $x_i$ 的“责任”，也叫“响应度”，记作 $γ_(ik)$，计算公式如下：

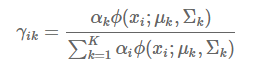
M步：根据样本和当前 γ 矩阵重新估计参数，注意这里 x 为列向量，计算公式如下：

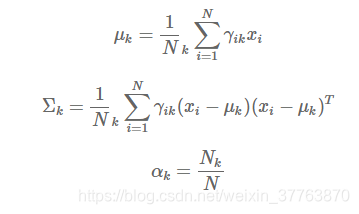
【目标】给定一堆没有标签的样本和模型个数 K，以此求得混合模型的参数，然后就可以用这个模型来对样本进行聚类。

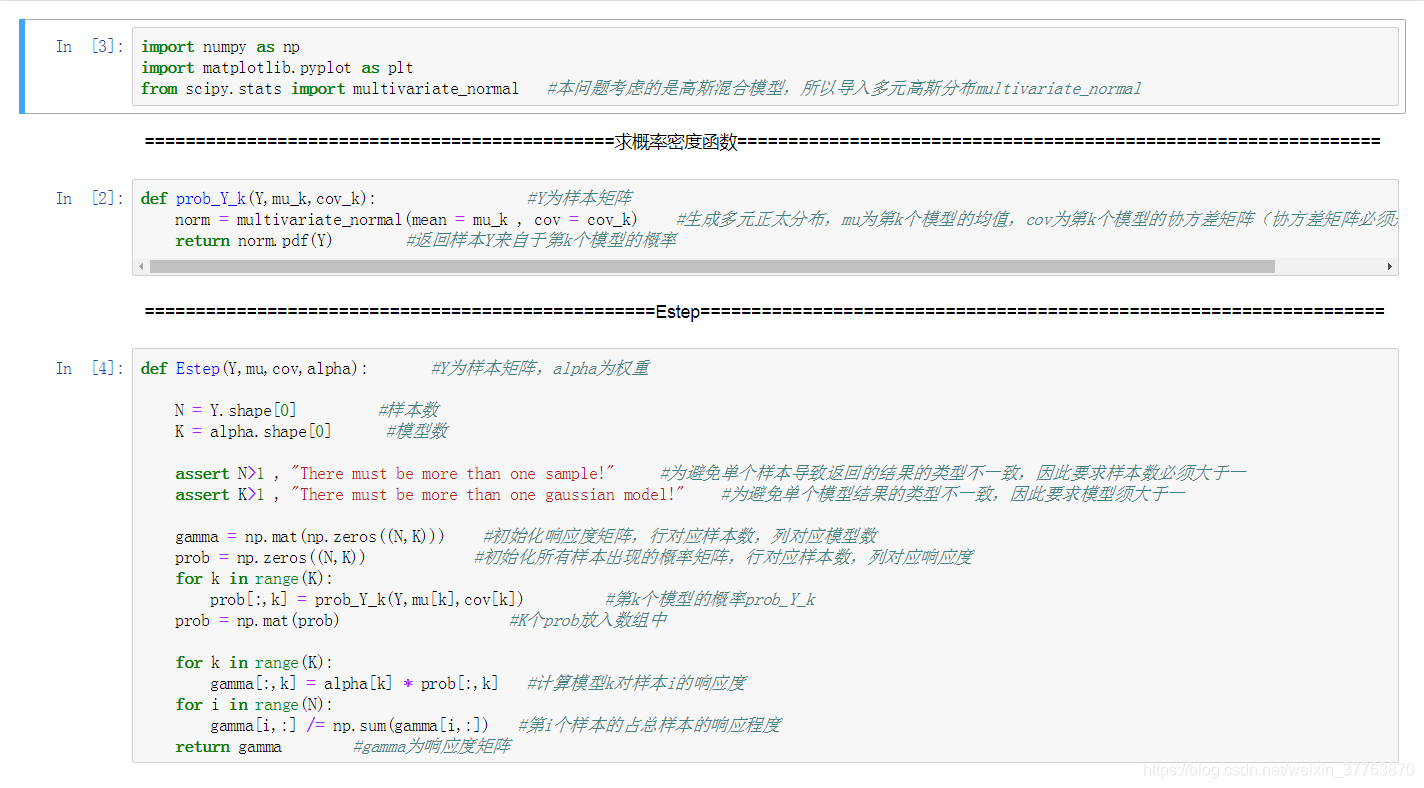
python代码如下：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal   #本问题考虑的是高斯混合模型，所以导入多元高斯分布multivariate_normal

def prob_Y_k(Y,mu_k,cov_k):                 #Y为样本矩阵
    norm = multivariate_normal(mean = mu_k , cov = cov_k)    #生成多元正太分布，mu为第k个模型的均值，cov为第k个模型的协方差矩阵（协方差矩阵必须是实对称矩阵）
    return norm.pdf(Y)        #返回样本Y来自于第k个模型的概率

def Estep(Y,mu,cov,alpha):       #Y为样本矩阵，alpha为权重
    
    N = Y.shape[0]         #样本数
    K = alpha.shape[0]      #模型数
    
    assert N>1 , "There must be more than one sample!"     #为避免单个样本导致返回的结果的类型不一致，因此要求样本数必须大于一
    assert K>1 , "There must be more than one gaussian model!"    #为避免单个模型结果的类型不一致，因此要求模型须大于一
    
    gamma = np.mat(np.zeros((N,K)))    #初始化响应度矩阵，行对应样本数，列对应模型数
    prob = np.zeros((N,K))            #初始化所有样本出现的概率矩阵，行对应样本数，列对应响应度
    for k in range(K):
        prob[:,k] = prob_Y_k(Y,mu[k],cov[k])         #第k个模型的概率prob_Y_k
    prob = np.mat(prob)                   #K个prob放入数组中
    
    for k in range(K):
        gamma[:,k] = alpha[k] * prob[:,k]   #计算模型k对样本i的响应度
    for i in range(N):
        gamma[i,:] /= np.sum(gamma[i,:])   #第i个样本的占总样本的响应程度
    return gamma        #gamma为响应度矩阵
   
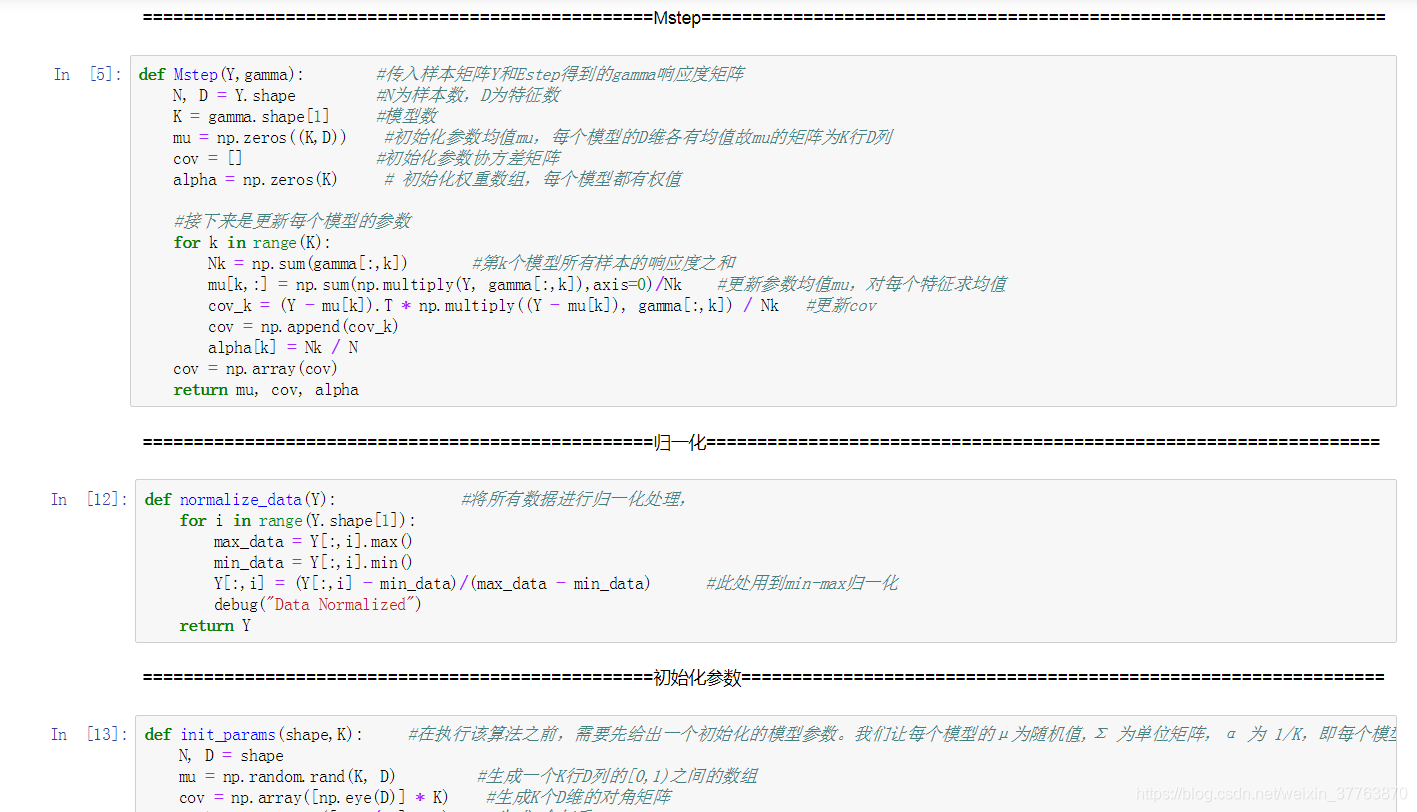
 def Mstep(Y,gamma):        #传入样本矩阵Y和Estep得到的gamma响应度矩阵
    N, D = Y.shape         #N为样本数，D为特征数
    K = gamma.shape[1]     #模型数
    mu = np.zeros((K,D))    #初始化参数均值mu，每个模型的D维各有均值故mu的矩阵为K行D列
    cov = []               #初始化参数协方差矩阵
    alpha = np.zeros(K)     # 初始化权重数组，每个模型都有权值
    
    #接下来是更新每个模型的参数
    for k in range(K):
        Nk = np.sum(gamma[:,k])       #第k个模型所有样本的响应度之和
        mu[k,:] = np.sum(np.multiply(Y, gamma[:,k]),axis=0)/Nk    #更新参数均值mu，对每个特征求均值
        cov_k = (Y - mu[k]).T * np.multiply((Y - mu[k]), gamma[:,k]) / Nk   #更新cov
        cov = np.append(cov_k)
        alpha[k] = Nk / N
    cov = np.array(cov)
    return mu, cov, alpha

def normalize_data(Y):              #将所有数据进行归一化处理，
    for i in range(Y.shape[1]):
        max_data = Y[:,i].max()
        min_data = Y[:,i].min()
        Y[:,i] = (Y[:,i] - min_data)/(max_data - min_data)      #此处用到min-max归一化
        debug("Data Normalized")
    return Y

def init_params(shape,K):     #在执行该算法之前，需要先给出一个初始化的模型参数。我们让每个模型的μ为随机值,Σ 为单位矩阵，α 为 1/K，即每个模型初始时都是等概率出现的。
    N, D = shape
    mu = np.random.rand(K, D)         #生成一个K行D列的[0,1)之间的数组
    cov = np.array([np.eye(D)] * K)    #生成K个D维的对角矩阵
    alpha = np.array([1.0 / K] * K)    #生成K个权重
    debug("Parameters initialized.")     
    debug("mu:",mu, "cov:",cov ,"alpha:",alpha,sep = "\n" )
    return mu, cov, alpha

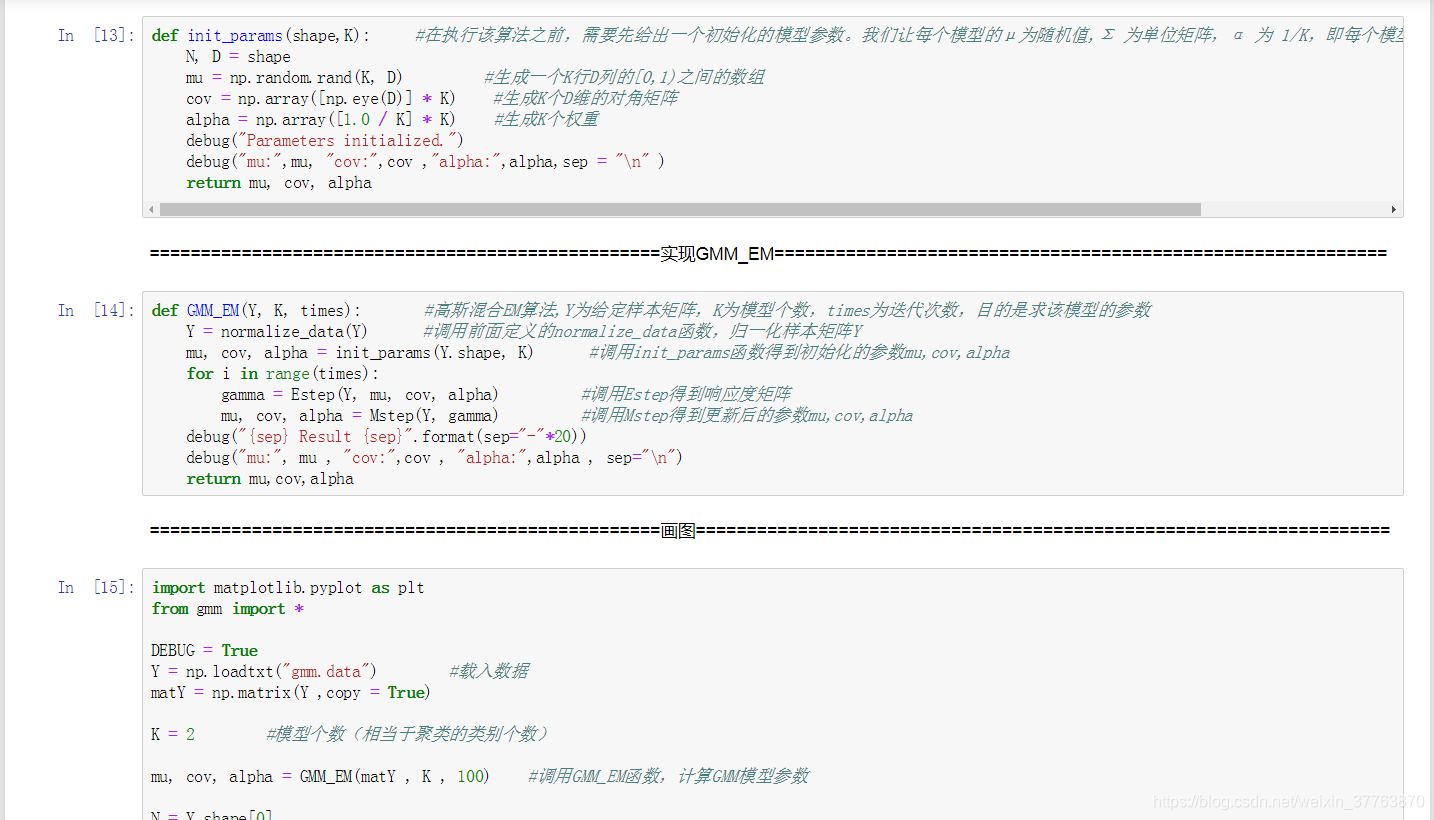
def GMM_EM(Y, K, times):       #高斯混合EM算法,Y为给定样本矩阵，K为模型个数，times为迭代次数，目的是求该模型的参数
    Y = normalize_data(Y)      #调用前面定义的normalize_data函数，归一化样本矩阵Y
    mu, cov, alpha = init_params(Y.shape, K)      #调用init_params函数得到初始化的参数mu,cov,alpha
    for i in range(times):
        gamma = Estep(Y, mu, cov, alpha)         #调用Estep得到响应度矩阵
        mu, cov, alpha = Mstep(Y, gamma)         #调用Mstep得到更新后的参数mu,cov,alpha
    debug("{sep} Result {sep}".format(sep="-"*20))
    debug("mu:", mu , "cov:",cov , "alpha:",alpha , sep="\n")
    return mu,cov,alpha

import matplotlib.pyplot as plt
from gmm import *

DEBUG = True 
Y = np.loadtxt("gmm.data")        #载入数据
matY = np.matrix(Y ,copy = True)

K = 2        #模型个数（相当于聚类的类别个数）

mu, cov, alpha = GMM_EM(matY , K , 100)    #调用GMM_EM函数，计算GMM模型参数

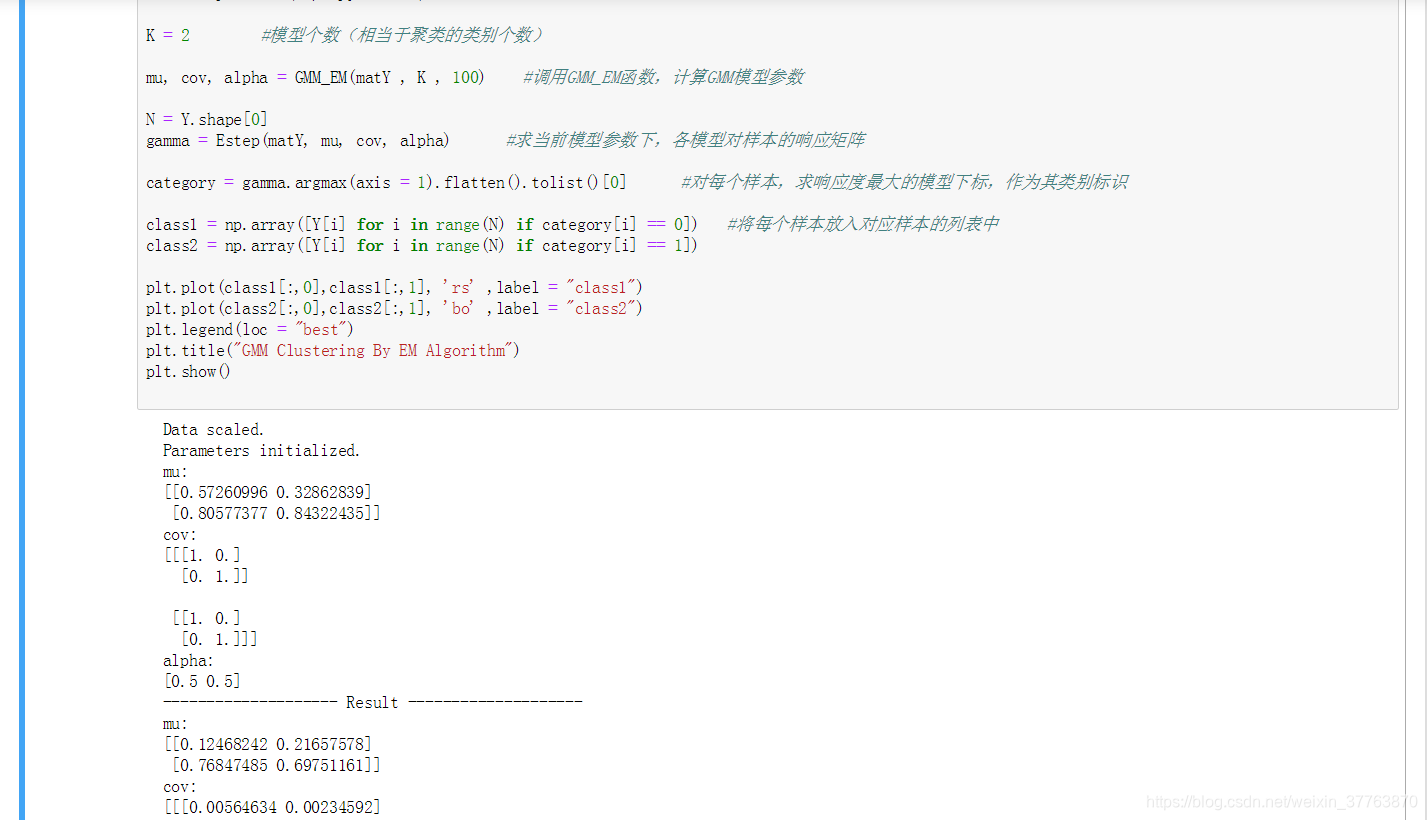
N = Y.shape[0]
gamma = Estep(matY, mu, cov, alpha)      #求当前模型参数下，各模型对样本的响应矩阵

category = gamma.argmax(axis = 1).flatten().tolist()[0]      #对每个样本，求响应度最大的模型下标，作为其类别标识

class1 = np.array([Y[i] for i in range(N) if category[i] == 0])   #将每个样本放入对应样本的列表中
class2 = np.array([Y[i] for i in range(N) if category[i] == 1])   

plt.plot(class1[:,0],class1[:,1], 'rs' ,label = "class1")
plt.plot(class2[:,0],class2[:,1], 'bo' ,label = "class2")
plt.legend(loc = "best")
plt.title("GMM Clustering By EM Algorithm")
plt.show()

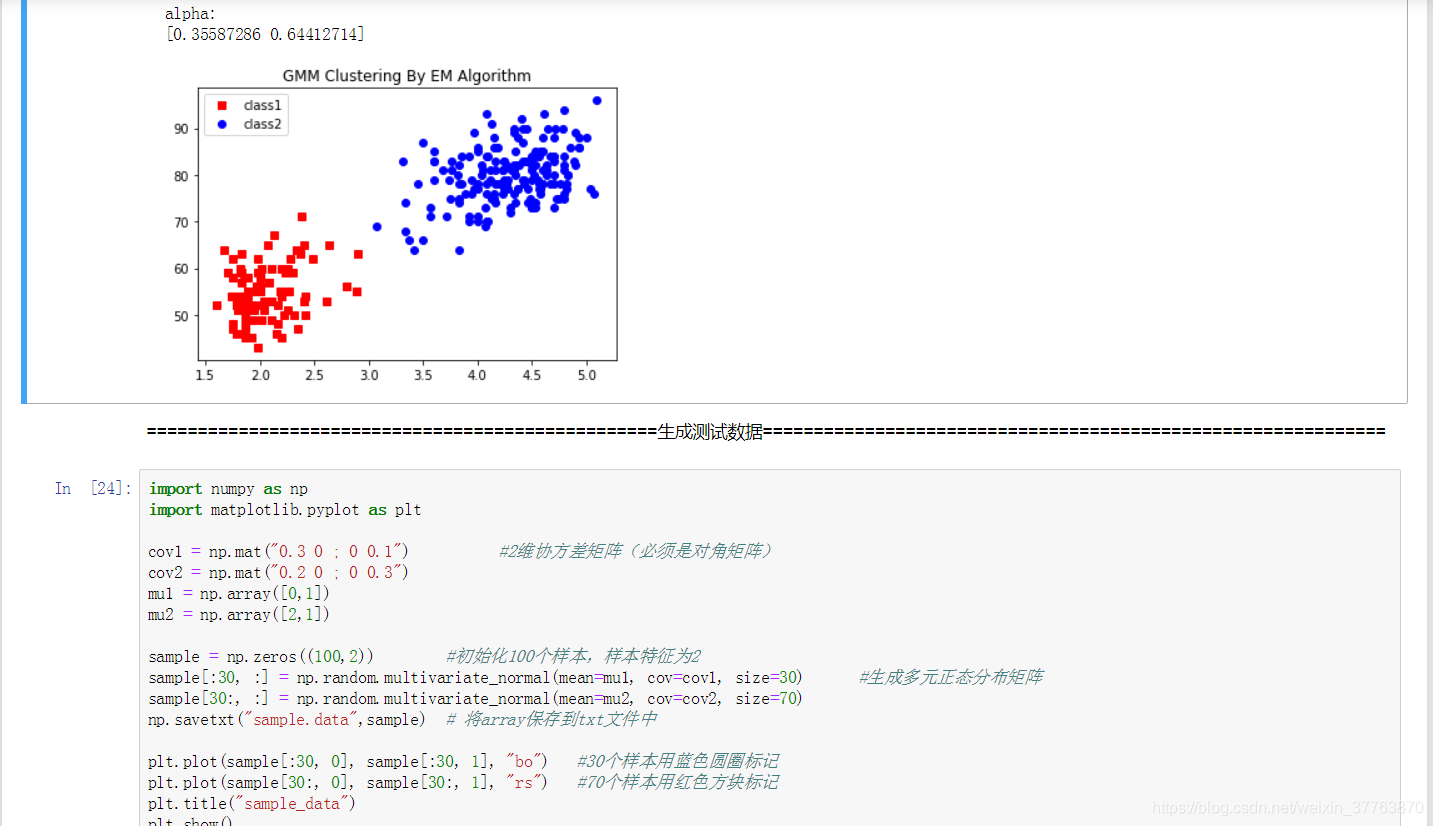
import numpy as np
import matplotlib.pyplot as plt

cov1 = np.mat("0.3 0 ; 0 0.1")          #2维协方差矩阵（必须是对角矩阵）  
cov2 = np.mat("0.2 0 ; 0 0.3")
mu1 = np.array([0,1])
mu2 = np.array([2,1])

sample = np.zeros((100,2))        #初始化100个样本，样本特征为2
sample[:30, :] = np.random.multivariate_normal(mean=mu1, cov=cov1, size=30)      #生成多元正态分布矩阵
sample[30:, :] = np.random.multivariate_normal(mean=mu2, cov=cov2, size=70)      
np.savetxt("sample.data",sample)  # 将array保存到txt文件中

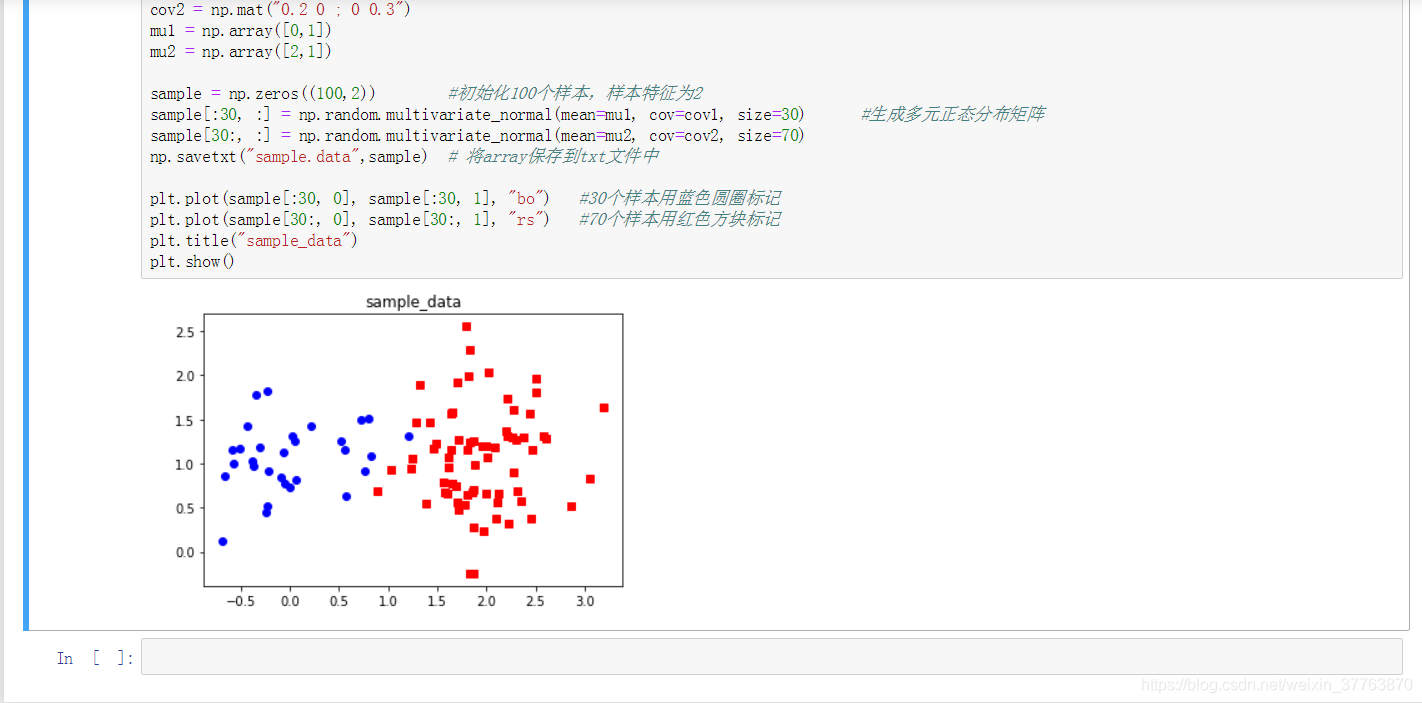
plt.plot(sample[:30, 0], sample[:30, 1], "bo")   #30个样本用蓝色圆圈标记
plt.plot(sample[30:, 0], sample[30:, 1], "rs")   #70个样本用红色方块标记
plt.title("sample_data")
plt.show()

效果：






【附】gmm.data链接
提取码：765t