傅里叶变换的公式:
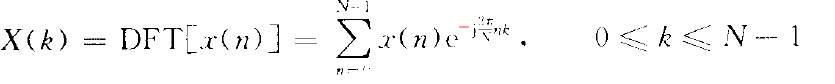
互相关的公式:
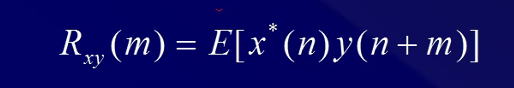
我们知道,对于一个正弦函数来说,其傅里叶变换的频谱出现一个峰,出现这个峰的原因是什么?下面用一个例子来说明

请注意,我在X(k),R(m)上面加了一条横线表示这并不是原公式,而是一种近似估计。从图中可以看出,傅里叶变换与相关运算很像。我们把傅里叶变换里的旋转因子项称为一系列的复正弦基函数,那么此时傅里叶变换就是在拿原序列和这一系列的基做类似于相关的运算。打个比方,把这一系列的基函数比做是你们班所有学生的照片,而x(n)是你的照片,那么在比对的时候无疑有一个匹配程度很高的照片,体现在频谱里就是出现一个峰。一个正弦函数做傅里叶变换,当轮到该序列与和它同频的复正弦基函数做相关时就会出现一个峰,出现这个峰的位置就是在该正弦函数的频率处,相当于是它自己与自己做了一个类似于自相关的运算。这个峰在DTFT的谱中就是其频率f(或w=2πf)处,理论上来说在DFT中,峰的横坐标乘以2π除以其DFT点数N等于其频率w,但实际上会有细微差距。
如果对这个频率参数的估计感兴趣的话可以参见下面这篇文章:
https://blog.csdn.net/naruhina/article/details/104697213
