基于粒子群算法的函数优化问题
一.算法简介
1.1思想来源
粒子群算法(Particle Swarm Optimization,PSO)是1995年提出的一种全局搜索算法,同时也是一种模拟自然界的生物活动以及群体智能的随机搜索算法,因其概念简明、实现方便、收敛速度快而为人所知。
粒子群算法的基本思想是模拟鸟群随机搜寻食物的捕食行为,鸟群通过自身经验和种群之间的交流调整自己的搜寻路径,从而找到食物最多的地点。其中每只鸟的位置/路径则为自变量组合,每次到达的地点的食物密度即函数值。每次搜寻都会根据自身经验(自身历史搜寻的最优地点)和种群交流(种群历史搜寻的最优地点)调整自身搜寻方向和速度,这个称为跟踪极值,从而找到最优解。
1.2基本原理
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟。
粒子仅具有两个属性:
速度:代表移动的快慢
位置:代表移动的方向。
每个粒子在搜索空间中单独的搜寻最优解,并将其记为当前个体极值,并将个体极值与整个粒子群里的其他粒子共享,找到最优的那个个体极值作为整个粒子群的当前全局最优解,粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。
速度和位置更新是粒子群算法的核心,其原理表达式和更新方式如下: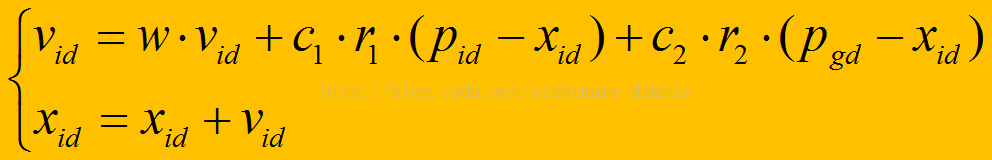
id:代数
X:位置
V:速度
w:惯性权重
c1:个体可信度
c2:群体可信度
r:随机数
二.基本流程
粒子群基本流程的主要分为:
1.参数初始化
2. 产生初始粒子和速度
3、寻找个体极值
4、寻找全局最优解
5、修改粒子的速度和位置
三.涉及参数
种群数量:影响算法的搜索能力和计算量。虽然初始种群越大收敛性会更好,不过太大了也会影响速度;
迭代次数:太少解不稳定,太多浪费时间。对于复杂问题,进化代数可以相应地提高;
惯性权重:该参数反映了个体历史成绩对现在的影响
加速系数:一般取0~2,此处要根据自变量的取值范围来定,分为个体和群体两种;
空间维数:粒子搜索的空间维数即为自变量的个数。
位置限制:限制粒子搜索的空间,即自变量的取值范围,对于无约束问题此处可以省略。
速度限制:如果粒子飞行速度过快,很可能直接飞过最优解位置,但是如果飞行速度过慢,会使得收敛速度变慢,因此设置合理的速度限制就很有必要了。
四.代码验证
1.加速系数与惯性因子
2.种群数量和空间维度
4.1 Griewank函数
此实验为验证三个最优值为0的多维函数
运行10次,每次迭代1000代 取平均值找到以下值的较好搭配:
二维图绘制:

4.1.1加速系数与惯性因子的探讨
在这里其他的参数为定值:
迭代次数:maxgen=1000;
种群规模:sizepop=200;
适应度函数维度:dim=10;
1.1 c1,c2为定值,w线性递减
c1 = 1.49445;
c2 = 1.49445;
w=-0.0007x+0.9(其中x为迭代次数1000,w随迭代次数从0.9到0.2线性变化)
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.00000 | 12.094 | 108 |
| 2 | 0.000000 | 12.060 | 96 |
| 3 | 0.000000 | 14.478 | 85 |
| 4 | 0.000000 | 12.348 | 113 |
| 5 | 0.000000 | 12.502 | 84 |
| 6 | 0.000000 | 13.415 | 104 |
| 7 | 0.000000 | 13.230 | 103 |
| 8 | 0.000000 | 12.573 | 89 |
| 9 | 0.000000 | 13.436 | 94 |
| 10 | 0.000000 | 12.346 | 97 |
| 平均值 | 0.000000 | 12.8428 | 98 |
1.2 c1线性递减,c2线性递增,w为定值
c1 = -0.0007x+0.9(其中x为迭代次数1000,c1随迭代次数从0.9到0.2线性变化)
c2 = 0.0007x+0.9(其中x为迭代次数1000,c2随迭代次数从0.2到0.9线性变化)
w=0.8
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 12.154 | 62 |
| 2 | 0.000000 | 12.504 | 63 |
| 3 | 0.000000 | 12.398 | 58 |
| 4 | 0.000000 | 15.531 | 61 |
| 5 | 0.000000 | 12.531 | 64 |
| 6 | 0.000000 | 12.668 | 65 |
| 7 | 0.000000 | 12.438 | 70 |
| 8 | 0.000000 | 12.458 | 58 |
| 9 | 0.000000 | 13.294 | 58 |
| 10 | 0.000000 | 12.392 | 57 |
| 平均值 | 0.000000 | 12.748 | 62 |
1.3 c1线性递减,c2线性递增,w线性递减
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 12.458 | 93 |
| 2 | 0.000000 | 12.686 | 93 |
| 3 | 0.000000 | 14.969 | 92 |
| 4 | 0.000000 | 13.452 | 95 |
| 5 | 0.000000 | 12.493 | 97 |
| 6 | 0.000000 | 12.305 | 96 |
| 7 | 0.000000 | 13.202 | 98 |
| 8 | 0.000000 | 12.467 | 95 |
| 9 | 0.000000 | 12.675 | 93 |
| 10 | 0.000000 | 13.245 | 93 |
| 平均值 | 0.000000 | 12.9679 | 95 |
小结
1.对于Griewank函数来说,以上三种情况下不论是从最有适应度还是运行时间与收敛的迭代次数来看,差别都不是很大。很可能是因为c1,c2即使是定值的时候也已经是一个较好的值了,所以差别不是非常大。如果c1,c2在之前没有用一个较好的值应该会有更明显的差别。
2.但是相对而言第二种情况,即随着迭代次数的增加c1线性递减,c2线性递增,w为定值0.8时运行速度最快,收敛的速度也最快,算法效果最好。
4.1.2种群数量和空间维度的探讨
在上述实验的基础上,采用c1,c2线性变化,w为定值不变的情况下
迭代次数为500
种群数量为200更改维度
2.1维度为10
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 7.179 | 62 |
| 2 | 0.000000 | 7.169 | 61 |
| 3 | 0000000 | 7.163 | 60 |
| 平均值 | 0.000000 | 7.170 | 61 |
2.2维度为20
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 7.464 | 168 |
| 2 | 0.000000 | 7.504 | 147 |
| 3 | 0.000000 | 6.975 | 169 |
| 平均值 | 0.000000 | 7.314 | 161 |
2.3维度为30
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 9.242 | 287 |
| 2 | 0.000000 | 7.551 | 287 |
| 3 | 0.000000 | 8.156 | 302 |
| 平均值 | 0.000000 | 8.316 | 292 |
小结
1.当维度增大时,运行时间会随着维度的增大而明显增大
2.当维度增大时,收敛代数也会明显增大
3.当维度增大时,解的空间范围变广,求解的难度变大,所以运算时间增大,收敛速度变慢
4.当维度在10-20之间,该函数的最优适应度值稳定在最优解
维度为10更改种群数量
2.1种群数量为100
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 4.968 | 87 |
| 2 | 0.000000 | 5.421 | 82 |
| 3 | 0000000 | 4.691 | 91 |
| 平均值 | 0.000000 | 5.026 | 86.6667 |
2.2种群数量为150
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 5.720 | 76 |
| 2 | 0.000000 | 5.482 | 60 |
| 3 | 0.000000 | 6.795 | 69 |
| 平均值 | 0.000000 | 5.9333 | 68.3333 |
2.3种群数量为200
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 7.179 | 62 |
| 2 | 0.000000 | 7.169 | 61 |
| 3 | 0000000 | 7.163 | 60 |
| 平均值 | 0.000000 | 7.170 | 61 |
小结
1.种群数量影响着算法的搜索能力和计算量
2.当种群数量增大时,计算量变大所以运行时间变长
3.当维度增大时,搜索能力增强所以收敛的代数变少,即收敛效率变高
4.当种群数量在150-200之间时候,该函数的最优适应度值稳定在最优解且运行效果较好
4.2 Rastrigin函数
二维图绘制:

4.2.1加速系数与惯性因子的探讨
在这里其他的参数为定值:
迭代次数:maxgen=1000;
种群规模:sizepop=200;
适应度函数维度:dim=10;
1.1 c1,c2为定值,w线性递减
c1 = 1.49445;
c2 = 1.49445;
w=-0.0007x+0.9(其中x为迭代次数1000,w随迭代次数从0.9到0.2线性变化)
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 6.964713 | 11.292 | 23 |
| 2 | 0.000000 | 11.715 | 280 |
| 3 | 0.000000 | 12.458 | 580 |
| 4 | 0.994959 | 12.402 | 620 |
| 5 | 0.000000 | 11.059 | 298 |
| 6 | 6.964713 | 11.348 | 50 |
| 7 | 0.004315 | 13.165 | 450 |
| 8 | 0.994974 | 11.392 | 860 |
| 9 | 0.000000 | 11.565 | 750 |
| 10 | 1.989918 | 13.907 | 602 |
| 平均值 | 1.7913592 | 12.0303 | 451 |
1.2 c1线性递减,c2线性递增,w为定值
c1 = -0.0007x+0.9(其中x为迭代次数1000,c1随迭代次数从0.9到0.2线性变化)
c2 = 0.0007x+0.9(其中x为迭代次数1000,c2随迭代次数从0.2到0.9线性变化)
w=0.8
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 13.456 | 825 |
| 2 | 0.000000 | 12.405 | 729 |
| 3 | 0.00000 | 12.548 | 880 |
| 4 | 0.000000 | 12.662 | 505 |
| 5 | 3.979836 | 12.649 | 795 |
| 6 | 0.994959 | 12.456 | 819 |
| 7 | 0.000006 | 12.127 | 1000 |
| 8 | 2.984878 | 12.231 | 997 |
| 9 | 1.989918 | 11.585 | 104 |
| 10 | 6.964713 | 12.319 | 301 |
| 平均值 | 1.6914 | 12.4711 | 696 |
1.3 c1线性递减,c2线性递增,w线性递减
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 2.989877 | 13.262 | 1000 |
| 2 | 0.000000 | 12.737 | 367 |
| 3 | 0.002861 | 12.549 | 1000 |
| 4 | 0.072869 | 12.260 | 999 |
| 5 | 4.974795 | 12.823 | 187 |
| 6 | 5.969754 | 12.282 | 154 |
| 7 | 0.000000 | 12.509 | 764 |
| 8 | 0.000000 | 12.570 | 807 |
| 9 | 5.969754 | 12.277 | 149 |
| 10 | 7.959672 | 12.198 | 553 |
| 平均值 | 5.5923 | 12.468 | 598 |
小结
1.对于Rastrigin函数来说,可以从图像看出有非常多的局部最优,所以算法在运行时也非常容易陷入局部最优,很难得到全局最小值。因为粒子群算法有随机性,所以总是过早的陷入局部最优,或者结果在最后仍然在震荡未趋于稳定。不论是这三种情况的哪一种,效果都不是非常理想。因为最终的最有适应度平均值最小也差1.69左右。
2.但是相对而言,也是第二种情况,即随着迭代次数的增加c1线性递减,c2线性递增,w为定值0.8时效果比其他两者好,虽然运行时间不是最短的,但是最优适应度函数是较其他两者优的。
4.2.2种群数量和空间维度
在上述实验的基础上,采用c1,c2线性变化,w为定值不变的情况下
迭代次数为500
种群数量为200更改维度
2.1维度为10
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.994959 | 7.411 | 403 |
| 2 | 7.959672 | 6.605 | 405 |
| 3 | 3.055519 | 7.416 | 500 |
| 平均值 | 4.00338 | 7.144 | 436 |
2.2维度为20
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 9.949591 | 6.561 | 359 |
| 2 | 3.979836 | 7.859 | 283 |
| 3 | 5.969754 | 6.975 | 169 |
| 平均值 | 6.643112 | 7.1316 | 270.3 |
2.3维度为30
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 10.944557 | 6.882 | 500 |
| 2 | 13.929433 | 6.966 | 487 |
| 3 | 0.994961 | 6.769 | 484 |
| 平均值 | 8.62298367 | 6.87233 | 490.33 |
小结
1.无论维度为多少,在当前参数的情况下,迭代500次都无法获得最优解
2.当维度增大时,所求得的最优解越来越不准确
3.当维度增大时,运行时间没有明显的增大
3.当维度增大时,收敛的代数也越来越趋于不稳定
维度为10更改种群数量
2.1种群数量为100
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 4.974795 | 5.434 | 287 |
| 2 | 5.969754 | 4.394 | 233 |
| 3 | 1.989918 | 4.268 | 155 |
| 平均值 | 4.311489 | 4.6986 | 225 |
2.2种群数量为150
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 3.979836 | 6.073 | 382 |
| 2 | 2.984877 | 5.763 | 275 |
| 3 | 2.002997 | 5.847 | 500 |
| 平均值 | 2.98917 | 3.87 | 385.667 |
2.3种群数量为200
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.994959 | 7.411 | 403 |
| 2 | 7.959672 | 6.605 | 405 |
| 3 | 3.055519 | 7.416 | 500 |
| 平均值 | 4.00338 | 7.144 | 436 |
小结
1.无论种群数量为多少,在当前参数的情况下,迭代500次都无法获得最优解
2.种群数量影响着算法的搜索能力和计算量
3.当种群数量增大时,计算量变大所以运行时间变长
4.当种群数量为200时,该函数在迭代500次左右仍然不能趋于稳定
5.该函数极容易陷入局部最优解
4.3 Schaffer函数
二维图绘制:

4.3.1加速系数与惯性因子的探讨
在这里其他的参数为定值:
迭代次数:maxgen=1000;
种群规模:sizepop=200;
适应度函数维度:dim=10;
1.1 c1,c2为定值,w线性递减
c1 = 1.49445;
c2 = 1.49445;
w=-0.0007x+0.9(其中x为迭代次数1000,w随迭代次数从0.9到0.2线性变化)
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 11.594 | 56 |
| 2 | 0.000000 | 11.542 | 36 |
| 3 | 0.000000 | 13.630 | 50 |
| 4 | 0.000000 | 11.138 | 25 |
| 5 | 0.000000 | 11.809 | 70 |
| 6 | 0.000000 | 12.575 | 60 |
| 7 | 0.000000 | 11.997 | 57 |
| 8 | 0.000000 | 11.667 | 63 |
| 9 | 0.000000 | 11.473 | 64 |
| 10 | 0.000000 | 11.672 | 58 |
| 平均值 | 0.000000 | 12.0688 | 54 |
1.2 c1线性递减,c2线性递增,w为定值
c1 = -0.0007x+0.9(其中x为迭代次数1000,c1随迭代次数从0.9到0.2线性变化)
c2 = 0.0007x+0.9(其中x为迭代次数1000,c2随迭代次数从0.2到0.9线性变化)
w=0.8
| # | 最优适应度 | 运行时间 | 大致收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 11.553 | 35 |
| 2 | 0.000000 | 11.263 | 28 |
| 3 | 0.000000 | 11.394 | 20 |
| 4 | 0.000000 | 12.239 | 24 |
| 5 | 0.000000 | 11.245 | 27 |
| 6 | 0.000000 | 11.394 | 29 |
| 7 | 0.000000 | 12.131 | 30 |
| 8 | 0.000000 | 11.432 | 32 |
| 9 | 0.000000 | 11.294 | 35 |
| 10 | 0.000000 | 11.223 | 23 |
| 平均值 | 0.00000 | 11.5168 | 28 |
1.3 c1线性递减,c2线性递增,w线性递减
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.00000 | 12.063 | 60 |
| 2 | 0.00000 | 11.084 | 34 |
| 3 | 0.00000 | 11.459 | 46 |
| 4 | 0.00000 | 11.395 | 31 |
| 5 | 0.00000 | 11.669 | 60 |
| 6 | 0.00000 | 11.468 | 68 |
| 7 | 0.00000 | 11.529 | 62 |
| 8 | 0.00000 | 11.234 | 68 |
| 9 | 0.00000 | 11.242 | 36 |
| 10 | 0.00000 | 11.456 | 63 |
| 平均值 | 0.00000 | 11.569 | 59 |
小结
1.对于Schaffer函数来说,同第一个函数一样,三者的性能相差不大,该算法对次函数的优化效果较好。
2.相对而言,同样是第二种情况,即随着迭代次数的增加c1线性递减,c2线性递增,w为定值0.8时效果比其他两者好,在较快时间和更小的收敛速度下得到最优值。
4.3.2种群数量和空间维度
在上述实验的基础上,采用c1,c2线性变化,w为定值不变的情况下
迭代次数为500
种群数量为200更改维度
2.1维度为10
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 6.125 | 41 |
| 2 | 0.000000 | 6.406 | 40 |
| 3 | 0000000 | 6.632 | 43 |
| 平均值 | 0.000000 | 6.3876667 | 41 |
2.2维度为20
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 6.128 | 28 |
| 2 | 0.000000 | 6.137 | 42 |
| 3 | 0.000000 | 6.450 | 45 |
| 平均值 | 0.000000 | 6.2383 | 38.33 |
2.3维度为30
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 6.982 | 36 |
| 2 | 0.000000 | 6.913 | 35 |
| 3 | 0.000000 | 6.507 | 26 |
| 平均值 | 0.000000 | 6.80066 | 32 |
小结
1.当维度增大时,运行时间会随着维度的增大而增大,但是不如第一个函数明显
2.当维度增大时,收敛代数会减小,收敛的速度变快
3.当维度在10-20之间,该函数的最优适应度值稳定在最优解
维度为10更改种群数量
2.1种群数量为100
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 4.312 | 51 |
| 2 | 0.000000 | 4.839 | 41 |
| 3 | 0000000 | 5.663 | 57 |
| 平均值 | 0.000000 | 4.938 | 49.6667 |
2.2种群数量为150
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 8.014 | 52 |
| 2 | 0.000000 | 5.861 | 32 |
| 3 | 0.000000 | 5.643 | 51 |
| 平均值 | 0.000000 | 6.506 | 45 |
2.3种群数量为200
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 1 | 0.000000 | 6.125 | 41 |
| 2 | 0.000000 | 6.406 | 40 |
| 3 | 0000000 | 6.632 | 43 |
| 平均值 | 0.000000 | 6.3876667 | 41 |
小结
1.种群数量影响着算法的搜索能力和计算量
2.当种群数量增大时,计算量变大所以运行时间变长
3.当维度增大时,搜索能力增强所以收敛的代数变少,即收敛效率变高
4.当种群数量在150-200之间时候,该函数的最优适应度值稳定在最优解且运行效果较好
五.与基于遗传算法的函数优化对比
粒子群算法和遗传算法(GA)都是优化算法,都力图在自然特性的基础上模拟个体种群的适应性,它们都采用一定的变换规则通过搜索空间求解。都是基于随机搜索的全局优化算法。 对高维复杂问题,往往会遇到早熟收敛和收敛性能差的缺点,都无法保证收敛到最优点。
5.1 Griewank函数的对比实验
当其他参数都在相对较优的情况下比较
维度相同且为20
种群数量为90
迭代次数为500
各运行十次后
算法与例子群优化算法的结果
1.遗传算法
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 平均值 | 0.000580 | 5.834 | 423 |
2.粒子群优化
| # | 最优适应度 | 运行时间 | 收敛代数 |
|---|---|---|---|
| 平均值 | 0.000000 | 4.503 | 218 |
小结
1.从实验结果来看,在迭代500次后粒子群优化算法的收敛速度速度和精确度要优于遗传算法。可见在稍高维度和种群数量较大的时候,该函数更适合用粒子群优化算法进行求解。
2.粒子群优化编码技术和遗传操作比较简单,不需要编码,没有交叉和变异操作,粒子只是通过内部速度进行更新,因此原理更简单、参数更少、实现更容易。
3.对于两节课的整体实验调参来看,粒子群优化算法对初始化参数的设置没有遗传算法那么敏感.
4. 两次实验的整体对比来看,粒子群优化算法更容易陷入局部最优解。
六.总结
粒子群算法是一种随机搜索算法 。
粒子的下一个位置受到自身历史经验和全局历史经验的双重影响,全局历史经验时刻左右着粒子的更新,群体中一旦出现新的全局最优,则后面的粒子立马应用这个新的全局最优来更新自己,大大提高了效率,相比与一般的算法(如遗传算法的交叉),这个更新过程具有了潜在的指导,而并非盲目的随机 。
自身历史经验和全局历史经验的比例尤其重要,这能左右粒子的下一个位置的大体方向,所以,粒子群算法的改进也多种多样,尤其是针对参数和混合其他算法的改进 。
总体来说,粒子群算法是一种较大概率收敛于全局最优解的,适合在动态、多目标优化环境中寻优的一种高效率的群体智能算法。
