#1182 : 欧拉路·三
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho破解了一道又一道难题,终于来到了最后一关。只要打开眼前的宝箱就可以通关这个游戏了。
宝箱被一种奇怪的机关锁住:
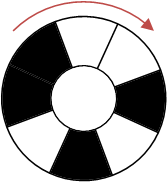
这个机关是一个圆环,一共有2^N个区域,每个区域都可以改变颜色,在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下,果然又发现了一个纸片:
机关黑色的部分表示为1,白色的部分表示为0,逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布,使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次,终究没有办法打开,只得在此写下机关破解之法。
——By 无名的冒险者
小Ho:这什么意思啊?
小Hi:我给你举个例子,假如N=3,我们通过顺时针转动,可以使得正下方的3个区域表示为:

因为黑色表示为1,白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域,可以得到一个新的数字。一共可以转动2N次,也就是2N个数字。我们要调整黑白区域的位置,使得这2^N个数字恰好是0~2 ^N-1
小Ho:我懂了。若N=2,则将环上的黑白色块调整为"黑黑白白",对应了"1100"。依次是"11",“10”,“00”,"01"四个数字,正好是0~3。那么这个"黑黑白白"就可以打开机关了咯?
小Hi:我想应该是的。
小Ho:好像不是很难的样子,我来试试!
提示:有向图欧拉回路
< 十分钟后 >
小Ho:啊啊啊啊啊,搞不定啊!
小Hi:怎么又是这样,你怎么做的?
小Ho:是这样的,每次转动一个区域不是相当于原来数字去掉最左边一位,并在最后加上1或者0么。于是我考虑对于"XYYY",它转动之后可以变成"YYY0"或者"YYY1"。我就将所有的数字0~2^N-1看作 2^N个点,连接所有的(“XYYY”,“YYY0”),(“XYYY”,“YYY1”)。比如当N=3时,我得到了这样一个图:

我要做的就是找一条路径,从一个点出发,走过所有的点后,再回到起点。但是我发现好像很难的样子。
小Hi:那当然了。你这样构造出来的路径叫做哈密顿回路,不是那么容易可以求解的。
小Ho:哎??那我应该怎么做。
小Hi:其实你的想法是没问题的,但是需要进行一下变换。在你的构图中我们是用点来表示数字,所以需要经过每一个点。如果我们用边来表示每一个数字呢?
小Ho:怎么用边表示数字?
小Hi:其实也很简单,比如说数字"10011",分别删掉它第一个数字和最后一个数字,得到"1001",“0011”。然后我们连接一条从"1001"到"0011"的有向边,表示数字"10011"。则我们可以得到构图的方法:
对于N,我们构造一个包含2^(N-1)个点和 2^N 条边的图,点的编号从0到2^(N-1)-1。编号为i的点表示数字i。对于任意两个点,如果点i,点j满足点i的后n-2个数字和点j的前n-2个数字相同,则我们连接有向边(i,j)。而边(i,j)表示了数字((i << 1)+(j & 1))。比如对于N=3的时候,我们可以得到:

可以很容易证明对于任意不同边(i,j),其表示的数字一定不同。
小Ho:这样构图话,只要找到一条欧拉回路就可以了。但是一定会有欧拉回路么?
小Hi:当然能了,对于有向图,其存在欧拉路的条件是,至多有两个点的入度不等于出度,且这两个点满足:其中一个点入度比出度多1,另一个点出度比入度多1。
若所有点的入度都等于出度,则一定存在欧拉回路。这可以通过和无向图欧拉路同样的方法进行构造证明。
而我们构造的图,由构造方法可以知道对于任意一个点,其入度一定为2,出度一定为2。所以它必定存在欧拉回路。
在有向图中找欧拉路的方法,也仍然可以使用Fleury算法。写成伪代码的话:
DFS(u):
While (以u为起点,且未被删除的边e(u,v))
删除边e(u,v)
DFS(v)
End
PathSize ← PathSize + 1
Path[ PathSize ] ← u
但是,有一点要注意,在使用Fleury算法计算有向图的欧拉路时,我们需要将path[]倒序输出才能得到正确的路径。
小Ho:那找到欧拉回路之后呢?
小Hi:找到欧拉回路之后只要对该条欧拉回路进行拼接就可以得到我们目标的圆盘状态了。
小Ho:好,我大概明白了。我这就来试试!
输入
第1行:1个正整数,N。1≤N≤15
输出
第1行:1个长度为2^N的01串,表示一种符合要
求的分布方案
样例输入
3
样例输出
00010111
相关知识点:
- 哈密顿通路:经过图(有向图和无向图)中** 所有顶点 一次且仅一次 的 通路**称作哈密顿通路。
- 。。。回路。。哈密顿回路,哈密顿回路也称哈密顿图。
- 。。。只有通路没有回路称半哈密顿图。
- 平凡图是哈密顿图。
定理: - 定理1:有向图是欧拉图 当且仅当它是强连通的 且 每一个顶点的 入度 等于 出度。
- 定理2:有向图是半欧拉图 当且仅当它是单向连通的 **且 恰有两个奇度顶点,其中一个顶点的入度比出度大1,另一个顶点的出度比入度大1,其余顶点入度等于出度。
思路:
这题很精妙,
整体题意就是我转一圈,能够得到0~(2^N - 1).
假设原来是xyz, x,y,z属于[0,1],转一下,就是:
xy(0 or 1) 或者(0 or 1)yz。
即:
xyz–>xy(0 or 1),
xyz–>(0 or 1)yz.
根据上述 转化规则 就可以构建出 点(xyz的十进制)与 点之间的关系,即可以根据点构造出有向图。
此时问题就是:一次有且一次走遍所有顶点(此时会想到哈密顿通路)
但是哈密顿通路目前没有很好的方法来求解。
此时精妙之处是把握住:只要转一圈能够得到所有0~(2^N - 1)的数字。
此时把顶点(数字)用边来表示,重新构造有向图。
之后就转化成了:走遍所有边一次且仅一次,即转化成找欧拉通路。
用边来表示顶点的规则:
是将 顶点num 的 二进制 最低位 去掉一位得到一个新的数字s,去掉二进制的最高位去掉一位得到e,此时用有向边:s—>e表示数字num。
num = s<<1 + (e&1)
本身要2^N - 1个顶点,现在就压缩成 2 ^ (N-1)个顶点, 2 ^ N - 1条边表示原来的顶点。
构造有向边,需要反推s,e:
num去掉最低位 : s = num >> 1
num去掉最高位(最高位是1的时候才是需要管的):
因为是0 ~ 2^N-1,N位二进制即可表示需要的数,
所以:t = (1<<(N-1)) - 1
(1先移到num最高位的位置,然后减一,使最高位变成0,其他位变成1,最后num&t就达到了去除最高位的效果)
e = num & t
构造边表示数字的无向图,跑一遍欧拉通路,
因为是有向图,所以最后结果要从(倒数第一位是回到了起点)倒数第二位逆序输出。(自己领悟:输出的 是每个二进制的 最低位 )
注意:
本题采用二维数组来标记边是不行的,1<<15 是 3e4+,
把握住fleury算法,删除走过的边(得子图),能不走桥就不走桥。
链式前向星存图,边 直接根据 边编号来 标记删除即可
AC代码:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5e4+5;
struct Edge
{
int to;
int nxt;
}edge[N];
int head[N>>1],idx;
bool vis[N];
int st[N],cnt;
void init()
{
//head[i]:最终记录与i相连的最后一条边的编号
//idx : 边起始编号
memset(head,0,sizeof(head));
idx = 1;
}
inline void add_edge(int from,int to)
{
edge[idx].to = to;
edge[idx].nxt = head[from];
head[from] = idx++;
}
void dfs(int s)
{
for(int i = head[s]; i; i = edge[i].nxt)
{
int to = edge[i].to;
//cout<<to<<endl;
//走过的边标记(i为边的编号)
if(vis[i]) continue;
vis[i] = true;
dfs(to);
}
st[cnt++] = s;
}
int main()
{
int n;
cin>>n;
int up = 1<< n;
init();
for(int i = 0; i < up; i++)
{
int x = i >> 1;
int t = (1<<(n-1))-1;
int y = i & t;
//cout<<i<<" "<<x<<" "<<y<<endl;
add_edge(x,y);
}
cnt = 0;
dfs(0);
for(int i = cnt-2; i >= 0; i--)
{
cout<<(st[i]&1);
}
cout<<endl;
return 0;
}
