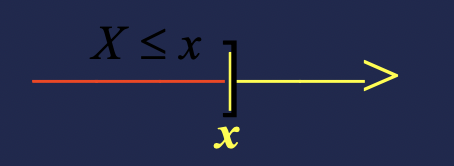1.随机试验、随机事件、样本空间

• 随机试验：每次出现的可能结果不止一个，且事先不能肯定会出现哪一个结果的试验

• 随机事件：在一次试验中可能发生也可能不发生的事件

  • 分类：
    • 基本事件：相对于观察目的不可再分解的事件
    • 复合事件：两个及以上基本事件合并
  • 随机事件的概率: $1 \geq P(A)\geq 0$表示事件A发生概率

• 样本点：随机试验的每个基本结果，记作 $e$

• 样本空间：全体样本点的集合，记作 $S$

e.g 掷骰子

$S=\{i:i=1,2,3,4,5,6\}$

2. 随机变量

• 随机变量：定义在样本空间上的实值函数，简称为 $r.v.$

  • 把随机试验结果数值化

  • 随试验结果的不同而取不同的值，在试验之前只知道它可能的取值范围，而不能预先肯定它将取的值

  • 由于试验结果的出现具有一定的概率，于是这种实值函数取每个值和每个确定范围内的值也有一定的概率。

  • 随机变量通常用大写字母表示 $X,Y,Z$或 $\zeta,\eta$，而随机变量所取的值，通常用小写字母 $x,y,z$表示
    

  • 分类：

    • 离散型随机变量：所有取值可以逐个一一列举
    • 连续型随机变量：全部可能取值无穷多

  • 随机事件与随机变量区别：

    1）随机变量包括随机事件

    2）随机变量是动态的观点，随机事件是静态的观点，如数学分析中常量与变量的区别

• 离散型随机变量

  • 离散型随机变量X的概率函数（或分布律，或概率分布）

    设 $x_k(k=1,2,...)$是离散型随机变量X所取的一切可能值，称
    $P(X=x_k)=p_k, k=1,2,...$
    其中 $p_k(k=1,2,...)$满足：

    (1) $p_k \geq 0,k=1,2,...$

    (2) $\sum_kp_k=1$

  • 离散型随机变量X的概率规律

  
  

  • 离散型随机变量由它的概率函数唯一确定

• 连续型随机变量

  • 连续型随机变量X的概率密度函数

    对于随机变量，如果存在非负可积函数 $f(x),x \in (-\infty,+\infty)$,使得对任意 $a \leq b$，有
    $P(a \leq X \leq b)=\int_a^bf(x)dx$
    则称X为连续型 $r.v$，称 $f(x)$为X的概率密度函数，简称为概率密度。

    其中 $f(x)$满足：

    （1） $f(x)\geq 0$

    （2） $\int_{-\infty}^{\infty}f(x)dx=1$

• 对 $f(x)$进一步理解：

  若 $x$是 $f(x)$的连续点，则：
  $lim_{\Delta x\to 0}\frac{p(x<X\leq x+\Delta x)}{\Delta x}=lim_{\Delta x\to0}\frac{\int_x^{x+\Delta x}f(t)dt}{\Delta x}=f(x)$
  故X的密度 $f(x)$在x这一点的值，恰好是X落在区间 $(x,x+\Delta x]$上的概率与区间长度 $\Delta x$之比的极限。这里，如果把概率理解为质量， $f(x)$相当于线密度。

  密度函数 $f(x)$在某点处 $a$的高度，并不反映X取值的概率。但是，这个高度越大，则X取 $a$附近的值的概率就越大。这说明某点密度曲线的高度反映了概率集中在该点附近的程度。

• 连续型随机变量取任一指定值的概率为0

  即： $P(X=a)=0$， $a$为任一指定值

  $\because P(x=a)=lim_{\Delta x \to 0}P(a\leq X<a+\Delta x)=lim_{\Delta \to 0}\int_a^{a+\Delta x}f(x)dx=0$

• 连续型随机变量唯一被它的密度函数所确定，所以，若已知密度函数，该连续型随机变量的概率规律就得到了全面描述

3.分布函数

• 背景：为了对离散型的和连续型的 $r.v$以及更广泛类型的 $r.v$给出一种统一的描述方法，引进了分布函数的概念。它是一个普通的函数，通过它，我们可以用数学分析的工具来研究随机变量。

• 定义：设X是一个 $r.v$，称

  $F(x)=P(X\leq x),(-\infty<x<+\infty)​$
  为 $X$的分布函数，记作 $X$~ $F(x)$或 $F_X(x)$。

  上式中 $X$是随机变量， $x$是参变量。 $F(x)$是随机变量 $X$取值不大于 $x$的概率。

  如果将X看作数轴上随机点的坐标，那么分布函数 $F(x)$的值就表示X落在区间 $(-\infty,x]$的概率。

  

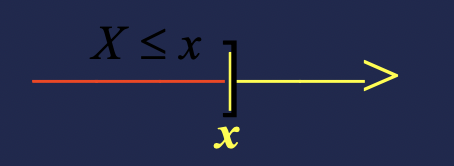
  对任意实数 $x_1<x_2$ ，随机点落在区间 $(x_1,x_2]$的概率为：
  $P\{x_1<X\leq x_2\}=P\{X\leq x_2\}-P\{X\leq x_1\}=F(x_2)-F(x_1)​$
  因此，只要知道了随机变量 $X$的分布函数，它的统计特性就可以得到全面的描述

• 分布函数的性质：

  （1） $F(x)$非降，即若 $x_1<x_2$，则 $F(x_1)\leq F(x_2)$

  （2） $F(-\infty)=lim_{x\to -\infty}F(x)=0$

  ​ $F(+\infty)=lim_{x\to +\infty}F(x)=1$

  （3） $F(x)$右连续，即 $lim_{x\to x_0^+}F(x)=F(x_0)$

• 离散型随机变量的分布函数

  设离散型随机变量 $X$的概率函数是
  $P\{X=x_k\}=p_k, \quad k=1,2,3,...$
  则
  $F(x)=P(X\leq x)=\sum_{x_k\leq x}p_k$
  由于 $F(x)$是 $X\leq x$的诸值 $x_k$的概率之和，故又称 $F(x)$为累积概率函数

• 连续型随机变量的分布函数

  若 $X$是连续型随机变量， $X$~ $f(x)$，则
  $F(x)=P(X\leq x)=\int_{-\infty}^xf(t)dt$
  即分布函数是密度函数的可变上限不定积分

  由上式可得，在 $f(x)$的连续点处，有
  $\frac{dF(x)}{dx}=f(x)$