用python 实现龙格-库塔（Runge-Kutta）方法

龙格-库塔法是1900年数学家卡尔-龙格和马丁-威尔海姆在1900年提出的一种求解非线性常微分方程的一种方法。本篇博客主要利用python语言实现龙格-库塔方法。
首先介绍龙格-库塔方法的公式：
已知，方程的导数和初值信息如下：

y^{'} = f (t, y), y (t_{0}) = y_{0}

$y' = f(t,y) , y(t_0)=y_0$
则方程的迭代计算公式如下：

y (t + Δ t) = y (t) + \frac{1}{6} (k_{1} + 2 k_{2} + 2 k_{3} + k_{4}) + O (Δ t^{4}) k_{1} = f (y, t) Δ t k_{2} = f (y + \frac{1}{2} k_{1}, t + \frac{1}{2} Δ t) Δ t k_{3} = f (y + \frac{1}{2} k_{2}, t + \frac{1}{2} Δ t) Δ t k_{4} = f (y + k_{3}, t + Δ t) Δ t

$y(t+\Delta t) = y(t)+\frac{1}{6}(k_1+2k_2+2k_3+k_4)+O(\Delta t^4)\\k_1 = f(y,t)\Delta t \\ k_2 = f(y+\frac{1}{2}k_1,t+\frac{1}{2}\Delta t) \Delta t \\ k_3 = f(y+\frac{1}{2}k_2,t+\frac{1}{2}\Delta t)\Delta t \\ k_4 = f(y+k_3,t+\Delta t) \Delta t$

现在举个例子，有一个方程、它的导数和初值如下：

y (t) = \frac{(t^{2} + 4)^{2}}{16} y^{'} (t) = \frac{t (t^{2} + 4)}{4} = t \sqrt{y (t)} y (0) = 1

$y(t) = \frac{(t^2+4)^2}{16}\\ y'(t)=\frac{t(t^2+4)}{4} = t\sqrt{y(t)}\\ y(0) = 1$
则利用龙格-库塔法拟合

y (t)

$y(t)$ 的python代码如下：

import math
import numpy as np
import matplotlib.pyplot as plt

def runge_kutta(y, x, dx, f):
    """ y is the initial value for y
        x is the initial value for x
        dx is the time step in x
        f is derivative of function y(t)
    """
    k1 = dx * f(y, t)
    k2 = dx * f(y + 0.5 * k1, x + 0.5 * dx)
    k3 = dx * f(y + 0.5 * k2, x + 0.5 * dx)
    k4 = dx * f(y + k3, x + dx)
    return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6.

if __name__=='__main__':
    t = 0.
    y = 1.
    dt = .1
    ys, ts = [], []
    def func(y, t):
        return t * math.sqrt(y)
    while t <= 10:
        y = runge_kutta(y, t, dt, func)
        t += dt
        ys.append(y)
        ts.append(t)

    exact = [(t ** 2 + 4) ** 2 / 16. for t in ts]
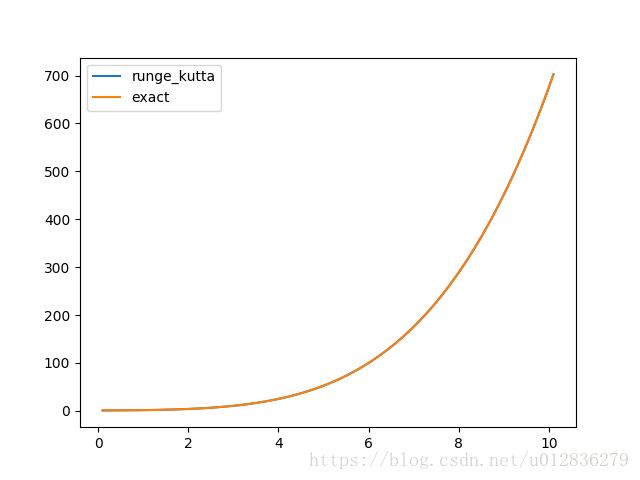
    plt.plot(ts, ys, label='runge_kutta')
    plt.plot(ts, exact, label='exact')
    plt.legend()
    plt.show()
    error = np.array(exact) - np.array(ys)
    print("max error {:.5f}".format(max(error)))

这段代码的运行结果如下：
这里写图片描述

用python 实现龙格-库塔（Runge-Kutta）方法

猜你喜欢