1. Discrete logarithm problem
Let 为 a known element of prime order in a group (with group operation written multiplicatively). Let be the group generated by .
常用的group选择有:
- multiplicative group of a finite field;
- algebraic torus over a finite field;
- elliptic curve over a finite field;
- divisor class group of a curve over a finite field。
Discrete logarithm problem常用假设有:
-
DLP: discrete logarithm problem。常用于Schnorr signatures, DSA signatures。
已知 ,找到 使得 。 -
CDH: computational Diffie-Hellman problem。常用于 Diffie-Hellman key exchange and variants, Elgamal encryption and variants, BLS signatures and variants。
已知 ,计算 。 -
SDH: static Diffie-Hellman problem。
Fix . Given ,计算 。 -
gap-CDH: Gap Diffie-Hellman problem。常用于 ECIES proof in the Random Oracle Model, Chaum undeniable signature。
已知 ,计算 ,when the algorithm has access to an oracle which solves the DDH problem。 -
DDH: decision Diffie-Hellman problem。常用于 Diffie-Hellman key exchange and variants, Elgamal encryption and variants.
已知 ,判断 是否成立? -
Strong-DDH: strong decision Diffie-Hellman problem
已知 ,判断 是否成立? -
sDDH: skewed decision Diffie-Hellman problem。
Let 为任意的uninvertible function with domain 。已知 ,判断 是否成立? -
PDDH: parallel decision Diffie-Hellman problem。
已知 ,判断 是否成立? -
Square-DH: Square Diffie-Hellman problem. The best known algorithm for Square-DH is to actually solve the DLP.
已知 ,计算 。 -
l-DHI: l-Diffie-Hellman inversion problem. The best known algorithm for l-DHI is to actually solve the DHP.
已知 ,计算 。 -
l-DDHI: l-Decisional Diffie-Hellman inversion problem
已知 ,判断 是否成立? -
REPRESENTATION: Representation problem. The best known algorithm for REPRESENTATION is to solve the DLP.
已知 ,找到 使得 成立。 -
LRSW: LRSW Problem. The best known algorithm for LRSW is to solve the DLP.
已知 ,已知 oracle (输入为 ,其选择一个随机值 ,然后其输出为 ),对于任意的 (not one of the 输入 )和 值 计算 。 -
Linear: Linear problem。The best known algorithm for Linear is to solve the DLP。
已知 ,计算 。 -
D-Linear1: Decision Linear problem (version 1)
已知 ,判断 是否成立? -
l-SDH: l-Strong Diffie-Hellman problem
已知 ,找到 并计算 。 -
c-DLSE: Discrete Logarithm with Short Exponents。The best known algorithm for the c-DLSE is to use the baby-step-giant-step or Pollard kangaroo algorithms for solving the DLP in a short interval. 常用于
Gennaro pseudorandom generator。
Let 其中 , 均为primes,let 为integer。已知 且 ,求解相应的 值。 -
CONF: (conference-key sharing scheme)。常用于Okamoto’s conference-key sharing scheme。
已知 ,计算 。 -
3PASS: 3-Pass Message Transmission Scheme。常用于Shamir’s 3-pass message transmission scheme。
已知 ,找到相应的 使得 成立。 -
LUCAS: Lucas Problem。
已知 ,找到相应的 ,使得 成立。其中 的定义为: -
XLP: x-Logarithm Problem。
对于Elliptic curve 上的任意一点 ,将 表示为 点$ X坐标的二进制表示。对任意的group element , ,是否能区分 和 ? -
MDHP: Matching Diffie-Hellman Problem。常用于E-Cash。
Let be a generator of group having order ,let and 。已知 和 ,找到相应的 。 -
DDLP: Double Discrete Logarithm Problem。常用于Public verifiable secret sharing。
Let 为素数且 ,设置 为group of order with generator , 为an element of order 。已知 ,求解 。 -
rootDLP: Root of Discrete Logarithm Problem。常用于Camenisch and Stadler group signature scheme。
已知group generator , positive integer 和 ,计算 使得 成立。 -
n-M-DDH: Multiple Decision Diffie-Hellman Problem。常用于 Group key exchange。
Let , 其中 为随机值; 为a random tuple in 。很难区分 和 。 -
l-HENSEL-DLP: l-Hensel Discrete Logarithm Problem。
Let 为a subgroup or prime order in ,其中 为a prime with polynomial binary length;Let be an integer满足 ,其中 。已知 , 为 范围内的随机数,计算 。 -
DLP(Inn(G)): Discrete Logarithm Problem over Inner Automorphism Group。常用于MOR Public Key Cryptosystem。
已知 for ,求解 。 -
IE: Inverse Exponent。
为l-DHI (l-Diffie-Hellman inversion problem) 的特例情况。 -
TDH: The Twin Diffie-Hellman Assumption。
Let 为 a cyclic group with generator ,and of prime order 。定义 ,其中 。定义twin DH function 。定义相应的twin DH predicate为: 。
twin DH assumption是指:已知random ,计算 很难。
strong twin DH assumption是指:已知 along with access to a decision oracle for the predicate which on input returns ,计算 很难。 -
XTR-DL: XTR discrete logarithm problem。Most protocols based on DLP can be used with XTR.
Let 为an XTR representation of an element of the XTR subgroup of ,已知 ,求解 使得 成立。 -
XTR-DH: XTR Diffie-Hellman problem。Most protocols based on DLP can be used with XTR.
Let 为an XTR representation of an element of the XTR subgroup of ,已知 ,求解 使得 成立。 -
XTR-DHD: XTR decision Diffie-Hellman problem.Most protocols based on DLP can be used with XTR.
Let 为an XTR representation of an element of the XTR subgroup of ,已知 ,判断 是否成立? -
CL-DLP: discrete logarithms in class groups of imaginary quadratic orders。常用于key exchange。
为standard discrete logarithm problems in a class group of imaginary quadratic orders。 -
TV-DDH: Tzeng Variant Decision Diffie-Hellman problem。常用于Conference key agreement.
Let 均为素数,let 为subgroup of order 。 为 内的整数, 为 内整数。已知 且 ,取任意整数 ,判断 是否成立? -
n-DHE: n-Diffie-Hellman Exponent problem。常用于 Broadcast encryption, accumulators.
对于a group of prime order ,let ,已知 ,计算
2. Factoring
- FACTORING: integer factorisation problem
- SQRT: square roots modulo a composite
- CHARACTERd: character problem
- MOVAd: character problem
- CYCLOFACTd: factorisation in Z[θ]
- FERMATd: factorisation in Z[θ]
- RSAP: RSA problem
- Strong-RSAP: strong RSA problem
- Difference-RSAP: Difference RSA problem
- Partial-DL-ZN2P: Partial Discrete Logarithm problem in Z∗n
- DDH-ZN2P: Decision Diffie-Hellman problem over Z∗n
- Lift-DH-ZN2P: Lift Diffie-Hellman problem over Z∗n
- EPHP: Election Privacy Homomorphism problem
- AERP: Approximate e-th root problem
- l-HENSEL-RSAP: l-Hensel RSA
- DSeRP: Decisional Small e-Residues in Z∗n2
- DS2eRP: Decisional Small 2e-Residues in Z∗n2
- DSmallRSAKP: Decisional Reciprocal RSA-Paillier in Z∗n2
- HRP: Higher Residuosity Problem
- ECSQRT: Square roots in elliptic curve groups over Z/nZ
- RFP: Root Finding Problem
- phiA: PHI-Assumption
- C-DRSA: Computational Dependent-RSA problem
- D-DRSA: Decisional Dependent-RSA problem
- E-DRSA: Extraction Dependent-RSA problem
- DCR: Decisional Composite Residuosity problem
- CRC: Composite Residuosity Class problem
- DCRC: Decisional Composite Residuosity Class problem
- GenBBS: generalised Blum-Blum-Shub assumption
3. Product groups
- co-CDH: co-Computational Diffie-Hellman Problem
- PG-CDH: Computational Diffie-Hellman Problem for Product Groups
- XDDH: External Decision Diffie-Hellman Problem
- D-Linear2: Decision Linear Problem (version 2)
- PG-DLIN: Decision Linear Problem for Product Groups
- FSDH: Flexible Square Diffie-Hellman Problem
- KSW1: Assumption 1 of Katz-Sahai-Waters
4. Pairings
2008年《Pairings for cryptographers》中指出,pairings over groups of known prime order 表示为:
若其中
都具有相同的prime order
,则可分为以下三大类:
1)Type 1:
;【通常使用supersingular curves,这些supersingular curves又分为两类:一类是over fields of characteristic 2 or 3 (with embedding degree 4 or 6 respectively);另一类是over fields of large prime characteristic (with embedding degree 2)。】
2)Type 2:
,但是存在efficiently computable homomorphism
;【通常使用ordinary curves,且the homomorphism from
to
is the trace map。】
3)Type3:
,且不存在efficiently computable homomorphism
。【通常使用ordinary curves,且
为the kernel of the trace map。】
若 为non-cyclic group of order ,则可称为Type 4。




具体举例为:
- Type 1:

- Type 2:

- Type 3:

若
,则表示为
。
Pairing 相关假设有:【注意,有的assumption并不适于所有的pairing type。Certain assumptions are provably false w.r.t. certain group types.】
-
BDHP: Bilinear Diffie-Hellman Problem。
已知 ,计算 。
其中 ,对应有四种可能的组合 ,也可称为 。
– 对于Type 1 pairing,以上四种组合是等价的。
– 对于Type 2 pairing,具有 。
– 对于Type 3 pairing,这四种组合have no known reductions between them。 -
DBDH: Decision Bilinear Diffie-Hellman Problem。常用于 Boneh-Franklin ID-based encryption scheme。
已知 ,判断 是否成立。 -
B-DLIN: Bilinear Decision-Linear Problem
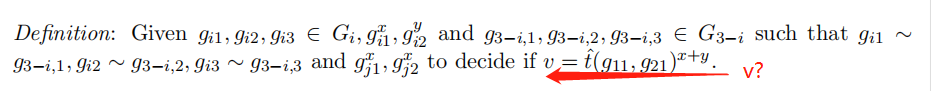
-
l-BDHI: l-Bilinear Diffie-Hellman Inversion Problem
已知 ,计算 。其中 。 -
l-DBDHI: l-Bilinear Decision Diffie-Hellman Inversion Problem
已知 和 ,判断 是否成立?其中 。 -
l-wBDHI: l-weak Bilinear Diffie-Hellman Inversion Problem。
已知 和 ,计算 。其中 。 -
l-wDBDHI: l-weak Decisional Bilinear Diffie-Hellman Inversion Problem
已知 和 ,判断 是否成立?其中 。 -
KSW2: Assumption 2 of Katz-Sahai-Waters。首次用于 the construction of a predicate encryption scheme supporting the inner product。(KATZ等人2008年论文《Predicate Encryption Supporting Disjunctions, Polynomial Equations, and Inner Products》)
– 运行 来获取 ;
– 设置 ,let 分别为 的generators;
– 选择随机数 以及random bit ;
– p.p.t. adversary 的输入有 和 ,当 时,再给 输入 ;当 时,给 的输入为a random element of 。 的输出为a bit ,且其succeed if 。 -
MSEDH: Multi-sequence of Exponents Diffie-Hellman Assumption。用于 Delerabl´ee and Pointcheval dynamic threshold public-key encryption scheme。
– Let 为a bilinear map group system,let 为3个整数,let 为 的generator, 为 的generator。
– 输入为2个random coprime polynomials 和 ,分别具有degree 和 ,分别具有pairwise distinct roots 和 。同时有 以及如下的exponentiations 序列:
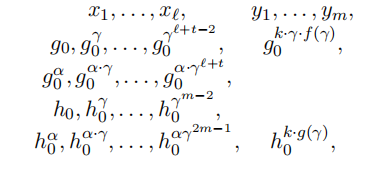
判断 是否与 相等或者与 中的某随机元素相同? -
SXDH assumption: the SXDH assumption states that there are prime-order groups that admits a bilinear map such that the Decisional Diffie-Hellman (DDH) assumption holds in both and . 首次在2005年论文《Correlation-Resistant Storage via Keyword-Searchable Encryption》中提出:

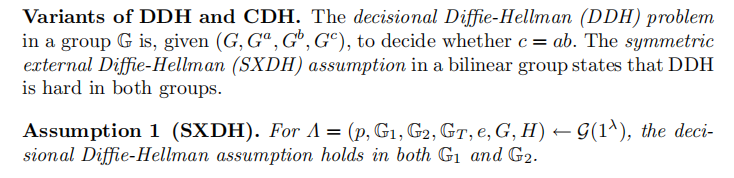
而在 2019年论文《Proofs for Inner Pairing Products and Applications》中指出,SXDH assumption仅在Type 3 pairings 下成立,因此任何基于SXDH assumption的设计均对应应采用Type 3 pairing。 -
DBP: double pairing assumption。在2016年论文《Structure-Preserving Signatures and Commitments to Group Elements》中提出。

5. Lattices
5.1 Main Lattice Problems
- SVPγp: (Approximate) Shortest vector problem
- CVPpγ: (Approximate) Closest vector problem
- GapSVPpγ: Decisional shortest vector problem
- GapCVPpγ: Decisional closest vector problem
5.2 Modular Lattice Problems
- SISp(n,m,q,β): Short integer solution problem
- ISISp(n,m,q,β): Inhomogeneous short integer solution problem
- LWE(n,q,φ): Learning with errors problem
5.3 Miscellaneous Lattice Problems
- USVPp(n,γ): Approximate unique shortest vector problem
- SBPp(n,γ): Approximate shortest basis problem
- SLPp(n,γ): Approximate shortest length problem
- SIVPp(n,γ): Approximate shortest independent vector problem
- hermiteSVP: Hermite shortest vector problem
- CRP: Covering radius problem
5.4 Ideal Lattice Problems
- Ideal-SVPf,pγ: (Approximate) Ideal shortest vector problem / Shortest polynomial problem
- Ideal-SISf,p q,m,β: Ideal small integer solution problem
6. Miscellaneous Problems
-
KEA1: Knowledge of Exponent assumption。参见2004年论文《The Knowledge-of-Exponent Assumptions and 3-Round Zero-Knowledge Protocols》:
背景知识为:Let be a prime such that is also prime, and let be a generator of the order subgroup of 。假设输入有 ,想要输出a pair 。可实现的方式之一是pick some ,设置 ,则有 成立。直观上来说,KEA1假设是指这是唯一的方式。对于任意的adversary能输出such a pair的,其肯定知道相应的 值使得 。在以下的正式定义中引入了extractor可返回相应的 值:
KEA1 (Knowledge of Exponent assumption) 的定义为: For any adversary that takes input ,返回 其中 ,即意味着存在an extractor ,对于与adversary相同的输入,可返回 值,使得 。 -
MQ: Multivariable Quadratic equations。多变量二次方程式。
已知a system of quadratic polynomial equations in variables each, ,求解 为 in general an NP-problem。 -
CF: Given-weight codeword finding。常用于: McEliece public key cryptosystem (finding the shortest codeword).
已知 binary linear code 和相应的 parity check matrix ,求解vector 使得 成立且 has weight 。 -
ConjSP: Braid group conjugacy search problem。
已知 ,求解 使得 成立。 -
GenConjSP: Generalised braid group conjugacy search problem。用于 Public-key cryptosystem due to Ko, Lee, Cheon, Han, Kang and Park。
已知 ,求解 使得 成立。 -
ConjDecomP: Braid group conjugacy decomposition problem。
已知 , for some ,求解 使得 成立。 -
ConjDP: Braid group conjugacy decision problem。
已知 ,判断 和 是否conjugate?即是否存在 使得 成立? -
DHCP: Braid group decisional Diffie-Hellman-type conjugacy problem。常用于 Public-key cryptosystem, pseudorandom number generator, pseudorandom synthesizer。
已知 ,判断 是否成立?for and 。 -
ConjSearch: (multiple simlutaneous) Braid group conjugacy search problem。
Let be a braid group, and be two tuples of elements of 。查找 使得 成立。 -
SubConjSearch: subgroup restricted Braid group conjugacy search problem。常用于Anshel- Anshel- Goldfeld key exchange protocol (AAG)。
Let be a braid group, and a subgroup of generated by some and let and be two tuples of elements of 。查找 , as a word in ,使得 成立。 -
LINPOLY : A linear algebra problem on polynomials。
Let be a linear space of dimension consisting of quadratic forms in variables 。已知 ,is it possible (and how) to uniquely determine ? For any subspace of the linear space generated by 。Let where is a finite field。
猜想:For randomly chosen , the probability that are very close to , when 。 -
HFE-DP: Hidden Field Equations Decomposition Problem。 It is the basis of the HFE crypto system.
Let be a finite field of order and be two invertible, affine transformations over the vector space 。Denote an extension field over and the bijection between this extension field and the corresponding vector space. We have 。
Now let for finite field elements the inner polynomial. This gives the public key:
or more precisely:
HFE Decomposition problem是指:已知公钥 ,找到对应的私钥 。 -
HFE-SP: Hidden Field Equations Solving Problem。
Let be a finite field of order and be two invertible, affine transformations over the vector space 。Denote an extension field over and the bijection between this extension field and the corresponding vector space. We have 。
Now let for finite field elements the inner polynomial. This gives the public key:
or more precisely:
Hidden Field Equations Solving Problem是指:已知 ,找到 使得 成立。 -
MKS: Multiplicative Knapsack。Naccache and Stern 用于构建 trapdoor one-way permutation。
已知正整数 以及a set ,找到a binary vector 使得 成立。 -
BP: Balance Problem。常用于Incremental hashing。
已知a group 和 a set ,找到disjoint subsets , not both empty,使得 成立。 -
AHA: Adaptive Hardness Assumptions.
We consider adaptive strengthenings of standard general hardness assumptions, such as the existence of one-way functions and pseudorandom generators.
– A collection of adaptive one-way functions is a family of functions such that for every , it is hard to invert for a random , even for an adversary that is granted access to an “inversion oracle” for for ever . In other words, the function is one-way, even with access to an oracle that invert all the functions in the family。
– A sf collection of adaptive pseudo-random generators is a family of functions such that for every , it is hard to invert is pseudo-random, even for an adversary that is granted access to an oracle whether given is in the range of for . -
SPI: Sparse Polynomial Interpolation。常用于Identification scheme。参见2000年论文《AN IDENTIFICATION SCHEME BASED ON SPARSE POLYNOMIALS》
已知 ,找到 a polynomial of degree at most 使得 for and has coefficients in 。 -
SPP: Self-Power Problem。若该问题可破解,在可伪造EIGamal signature scheme中类型2和4的签名。
已知prime 和 ,求解 。 -
VDP: Vector Decomposition Problem。常用于AN IDENTIFICATION SCHEME BASED ON SPARSE POLYNOMIALS,AN IDENTIFICATION SCHEME BASED ON SPARSE POLYNOMIALS。
已知a two-dimensional vector space over a finite field, with basis ,和 a vector in 。找到 a multiple of 使得 is a multiple of 。 -
2-DL: 2-generalized Discrete Logarithm Problem。
已知a group of exponent and order , with generators , and an element in 。找到 a pair of integers 使得 成立。
参考资料
[1] Can you give me a summary of cryptographic hardness assumptions?
[2] 2013年报告《Final Report on Main Computational Assumptions in Cryptography》
[3] European Network of Excellence in Cryptology II
[4] 2012年 Cryptographic Primitives and Hard Problems in Cryptography wiki
[5] 2015年论文《Cryptographic Assumptions: A Position Paper》