目录
一般高斯情况下Fisher信息阵公式
一般高斯情况时，即：
那么x的概率密度函数可以表示为：
其中：
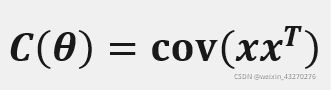
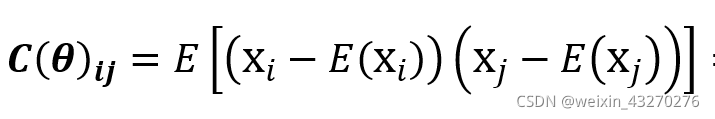
其中μ(θ)和C(θ)都存在待估计的参数，且C(θ)是对称矩阵
那么一般高斯情况时，Fisher信息矩阵的第i，j个元素，可以表示为：
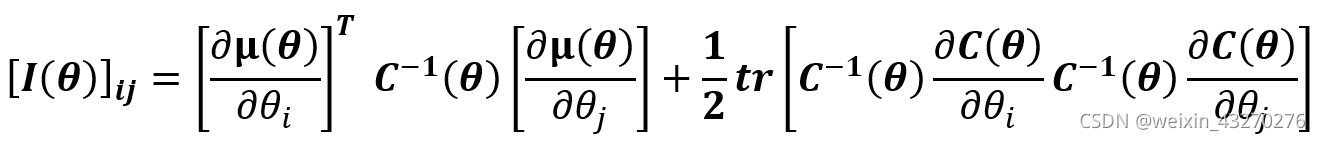
公式推导前需要整理的公式和性质
性质1：自相关矩阵和其逆矩阵都是对称矩阵
是对称矩阵，且
也是对称矩阵
具体可以参考：
https://blog.csdn.net/weixin_43270276/article/details/120560885?spm=1001.2014.3001.5501
性质2：行列式求导公式
性质3：逆矩阵求导公式
具体参考：
笔记：矩阵行列式求导以及矩阵的逆的求导_DengTseng的博客-CSDN博客_矩阵行列式求导
性质4：向量求迹(Tr)
对于相同长度的矢量m和n，那么存在：
性质5：对称阵的计算公式
其中：
性质6：正态分布的奇数阶矩为0
参考
标准正态分布k阶原点矩公式_犹有傲霜枝的博客-CSDN博客_正态分布的k阶原点矩
证明过程
第一步：写出包含待估计量的似然函数
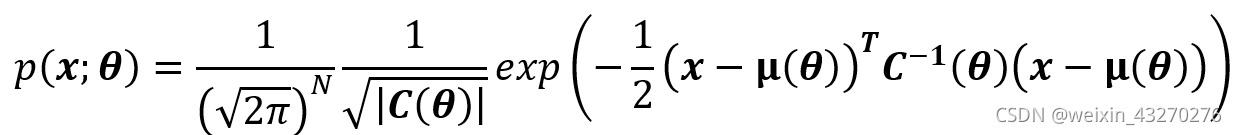
第二步：对似然函数求对数
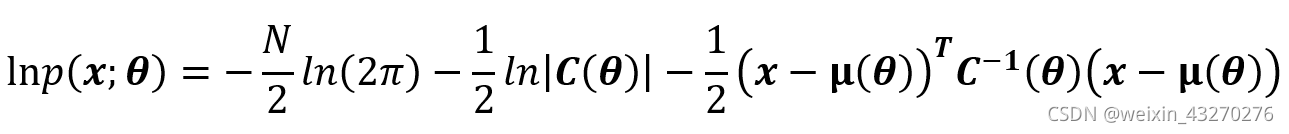
第三步：求一阶导数
上式计算时，分三部分，显然第一项不包含待估计参数θ，所以该项对所有待估计参数的一阶导数都为0。因此重点要求第二和第三项对待估计参数的一阶导数。
第二项对待估计参数的一阶导数：
由于是N*N维矩阵，因此
也是N*N维矩阵，根据上述性质2，得到：
第三项对待估计参数的一阶导数：
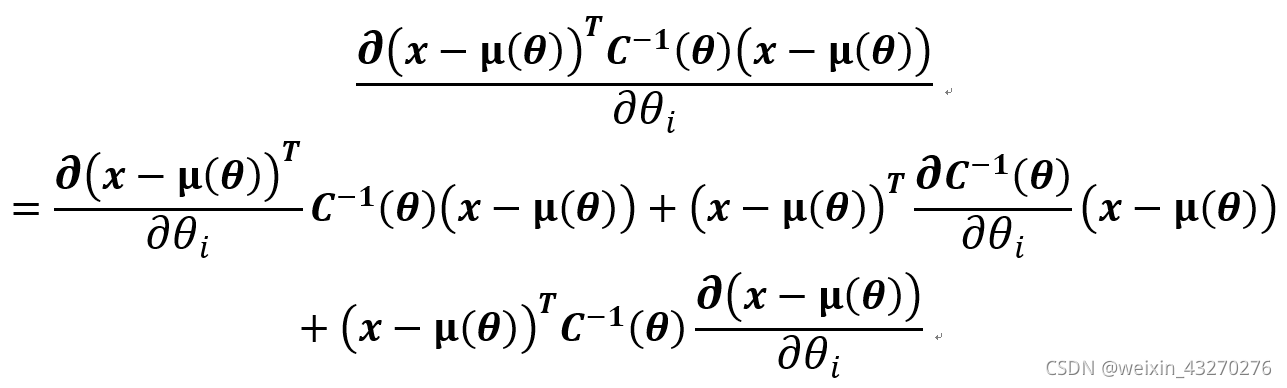
而其中：
因此第三项对待估计参数的一阶导数可以表示为：
因此，最终一阶导数可以表示为：
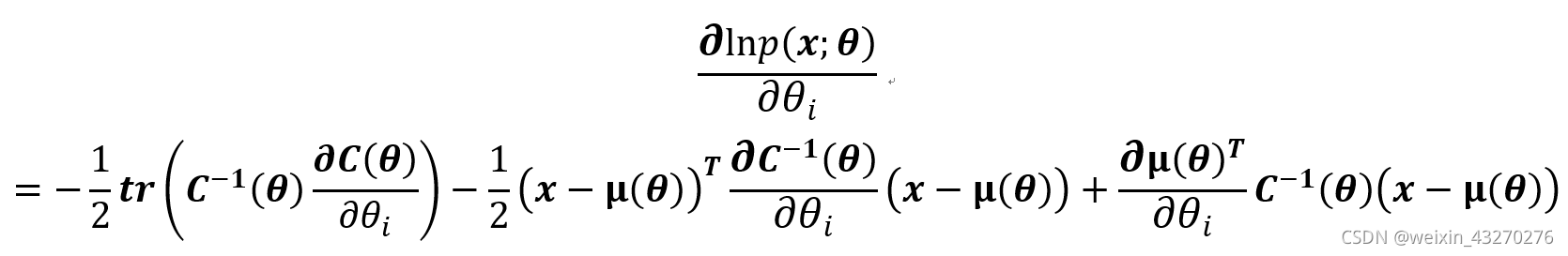
第四步：求Fisher矩阵
利用统计信号处理基础（3-23）性质，得到：
为了简化运算过程，令：
因此：
于是可以得到：
利用性质6，可以得到上式中：
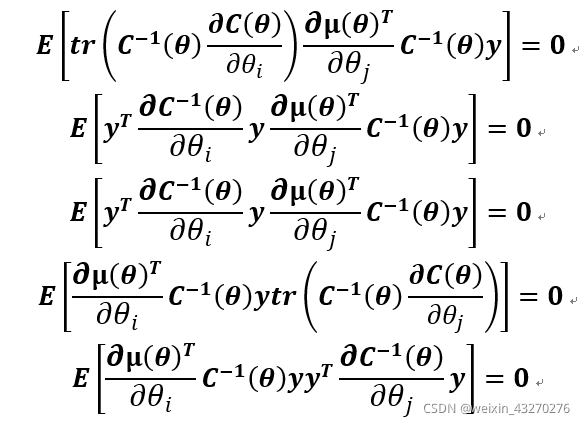
因此，可以稍微简化为：
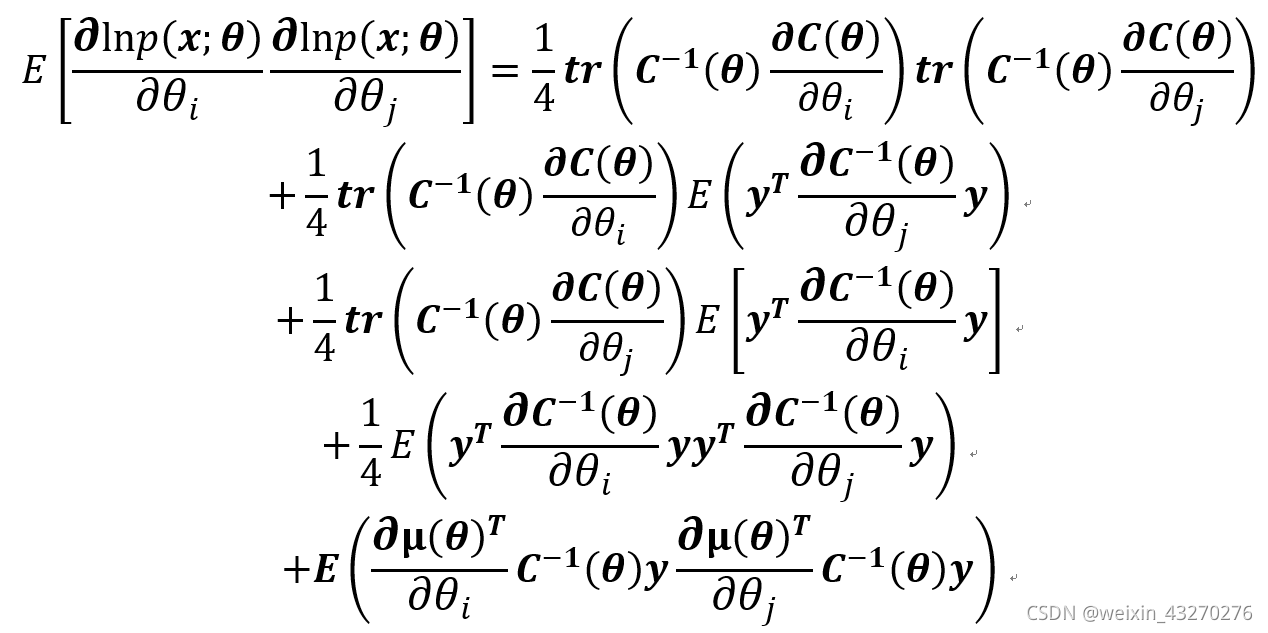
上式中的第一项不需要化简，而第二第三项的化简，需要用到性质3和性质4，具体为：
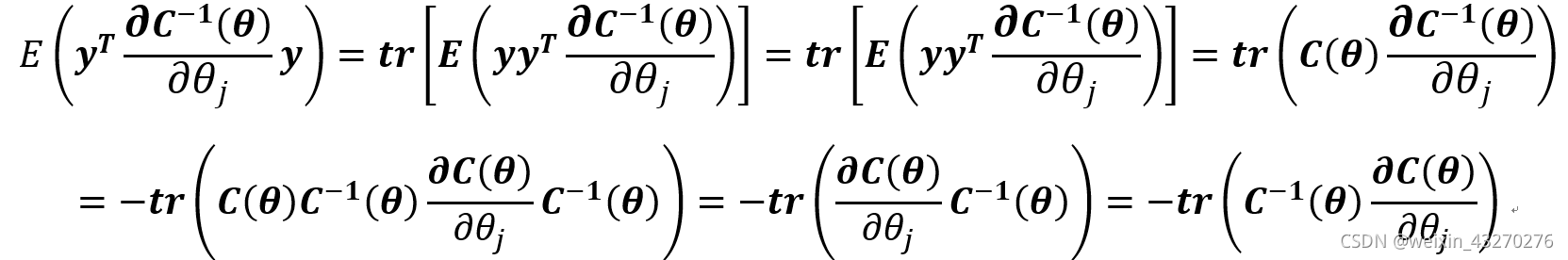
同理：
因此，第二第三项可以化简为：
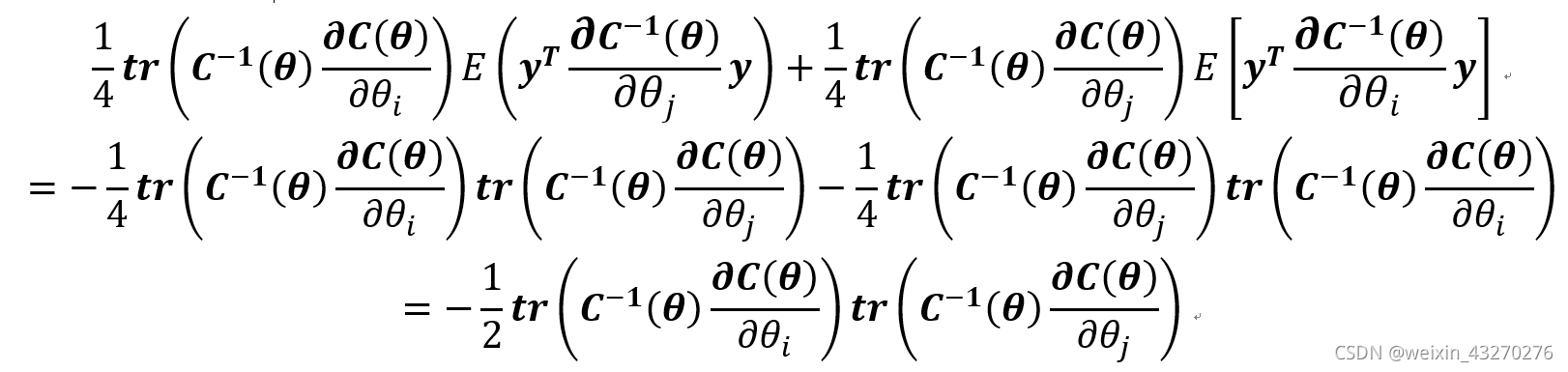
第四项的化简，需要用到性质5
第五项的化简：
由于：
和
都是1*1的元素，因此：
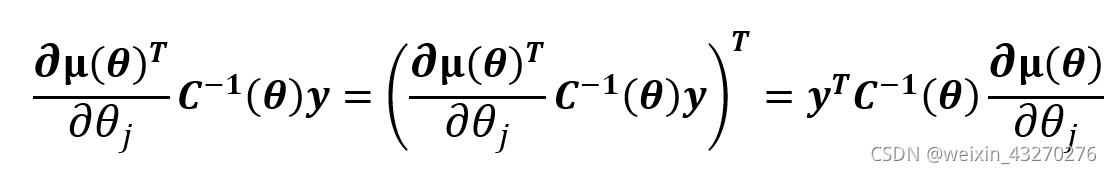
于是：
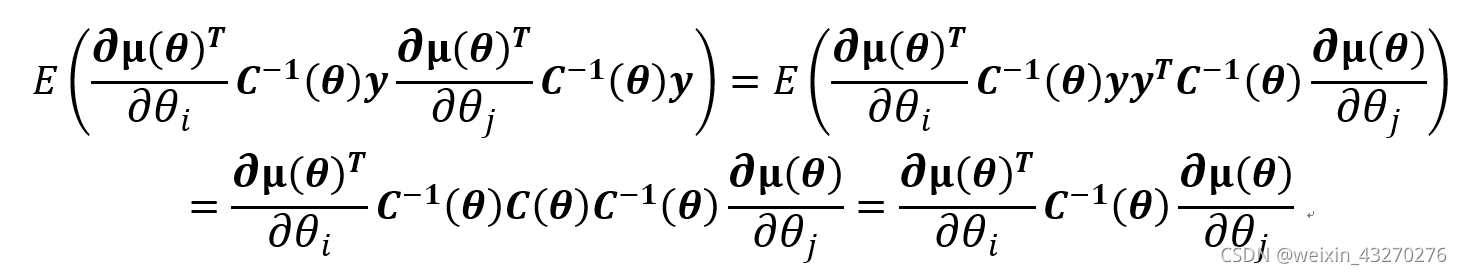
上述化简代入后，最终可以得到：
证明完毕。