①
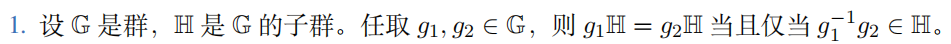
(1)
充分性:
g 1 H = g 2 H , 则 存 在 h 1 , h 2 ∈ H 使 得 g 1 h 1 = g 2 h 2 g_1H = g_2H, 则存在 h_1, h_2 ∈ H 使得 g_1h_1 = g_2h_2 g1H=g2H,则存在h1,h2∈H使得g1h1=g2h2
即 得 g 2 = g 1 h 1 h 2 − 1 , g 1 − 1 g 2 = g 1 − 1 g 1 h 1 h 2 − 1 = h 1 h 2 − 1 ∈ H 即得 g_2 = g_1h_1h_2^{-1}, g_1^{-1}g_2 = g_1^{-1}g_1h_1h_2^{-1} = h_1h_2^{-1} ∈ H 即得g2=g1h1h2−1,g1−1g2=g1−1g1h1h2−1=h1h2−1∈H
(2)
必要性:
若 有 g 1 − 1 g 2 ∈ H , 则 g 1 g 1 − 1 g 2 ∈ g 1 H , 即 g 2 ∈ g 1 H 若有g_1^{-1}g_2∈H,则g_1g_1^{-1}g_2∈g_1H,即g_2∈g_1H 若有g1−1g2∈H,则g1g1−1g2∈g1H,即g2∈g1H
由 命 题 8.1 可 得 g 1 H = g 2 H 由命题8.1可得g_1H = g_2H 由命题8.1可得g1H=g2H
②
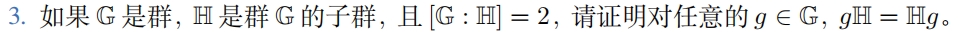
[G : H] = 2, 所以存在 g 使得 G 被划分为 H 与 gH.
而当 g ∈ H 时, gH = Hg = H
当 g ∉ H 时, gH != H, Hg != H, 则 gH = Hg 都在另一个划分上
③
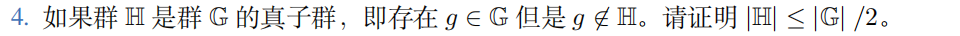
设 g_1 ∈ G 且 g_1 ∉ H, g_2 ∈ H, 设 h ∈ H, 则有 g_1h != g_1h, 即 g_1H != g_2H, 即 [G : H] >= 2, |G|/2 >= |H|
④
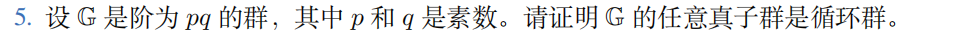
设 H 为 G 的真子群, h ∈ H, 则由拉格朗日定理可得 ord(h) | pq, 则 H 的阶为 p 或 q, 由推论8.2可得 H 为循环群
⑤

(1)
费 尔 马 小 定 理 : a p − 1 ≡ 1 ( m o d p ) ( p 为 素 数 且 p 不 整 除 a ) 费尔马小定理:a^{p-1}≡1(modp)(p为素数且p不整除a) 费尔马小定理:ap−1≡1(modp)(p为素数且p不整除a)
现有整数模 p 下的乘法群 Z_p^{*}. 设 a ∈ Z_p^{*} 由拉格朗日定理得 ord(a) | p-1, 设 p-1 = n*ord(a), 那么有
a p − 1 = a n ∗ o r d ( a ) ≡ 1 ( m o d p ) a^{p-1}=a^{n*ord(a)}≡1(modp) ap−1=an∗ord(a)≡1(modp)
(2)
欧 拉 定 理 : a φ ( m ) ≡ 1 ( m o d m ) ( g c d ( a , m ) = 1 ) 欧拉定理:a^{φ(m)}≡1(modm)(gcd(a,m)=1) 欧拉定理:aφ(m)≡1(modm)(gcd(a,m)=1)
现有整数模 p 下的乘法群 Z_p^{*}. 设 a ∈ Z_p^{*} 由拉格朗日定理得 ord(a) | φ(m), 设 φ(m) = n*ord(a), 那么有
a φ ( m ) = a n ∗ o r d ( a ) ≡ 1 ( m o d m ) a^{φ(m)}=a^{n*ord(a)}≡1(modm) aφ(m)=an∗ord(a)≡1(modm)