
第3题
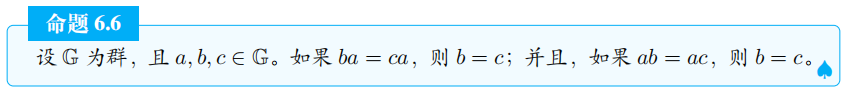
①
若 ba = ca, 则 baa^{-1} = caa^{-1}. 所以 be = ce, 又因为群有 ae = ea = a, 则 b = c;
②
若 ab = ac, 则由乘法交换律得 ab = ba, ac = ca, 所以有 ba = ca, 由①得 b = c.
第4题

①
g m g n g^{m}g^{n} gmgn
= g ⋅ g ⋅ ⋅ ⋅ g ( m − 1 次 群 运 算 ) g ⋅ g ⋅ ⋅ ⋅ g ( n − 1 次 群 运 算 ) =g·g···g(m-1次群运算)g·g···g(n-1次群运算) =g⋅g⋅⋅⋅g(m−1次群运算)g⋅g⋅⋅⋅g(n−1次群运算)
= g ⋅ g ⋅ ⋅ ⋅ g ( m + n − 1 次 群 运 算 ) =g·g···g(m+n-1次群运算) =g⋅g⋅⋅⋅g(m+n−1次群运算)
= g m + n =g^{m+n} =gm+n
②
( g m ) n (g^{m})^{n} (gm)n
= g m ⋅ g m ⋅ ⋅ ⋅ g m ( n − 1 次 群 运 算 ) =g^{m}·g^{m}···g^{m}(n-1次群运算) =gm⋅gm⋅⋅⋅gm(n−1次群运算)
= g m + m + ⋅ ⋅ ⋅ + m ( n − 1 次 加 法 运 算 ) =g^{m+m+···+m(n-1次加法运算)} =gm+m+⋅⋅⋅+m(n−1次加法运算)
= g m n =g^{mn} =gmn
③
( g h ) n (gh)^{n} (gh)n
= ( ( ( g h ) − 1 ) − 1 ) n =(((gh)^{-1})^{-1})^{n} =(((gh)−1)−1)n
由②可得
= ( ( g h ) − 1 ) − n =((gh)^{-1})^{-n} =((gh)−1)−n
= ( h − 1 g − 1 ) − n =(h^{-1}g^{-1})^{-n} =(h−1g−1)−n
= g n h n =g^{n}h^{n} =gnhn
第5题
设群的阶为 2n
则 群 中 必 有 一 元 素 a , 使 得 a 2 n = ( a n ) 2 = e 则群中必有一元素 a, 使得a^{2n}=(a^{n})^{2}=e 则群中必有一元素a,使得a2n=(an)2=e
则存在
g = a n g = a^{n} g=an
第6题

必要性证明:
∀ a ∈ H , 存 在 单 位 元 e = a a − 1 ∈ H ∀a∈H,存在单位元e=aa^{-1}∈H ∀a∈H,存在单位元e=aa−1∈H
∀ a ∈ H , 存 在 e a − 1 = a − 1 ∈ H , 故 逆 元 存 在 ∀a∈H,存在ea^{-1}=a^{-1}∈H,故逆元存在 ∀a∈H,存在ea−1=a−1∈H,故逆元存在
∀ a , b ∈ H , 由 上 述 逆 元 , ∃ b − 1 ∈ H , 则 a b = a ( b − 1 ) − 1 ∈ H , 故 有 封 闭 性 ∀a,b∈H,由上述逆元,∃b^{-1}∈H,则ab=a(b^{-1})^{-1}∈H,故有封闭性 ∀a,b∈H,由上述逆元,∃b−1∈H,则ab=a(b−1)−1∈H,故有封闭性
结 合 律 显 然 结合律显然 结合律显然
故必要性得证。
第7题
条 件 : G 是 群 , ∀ n ∈ N , i ∈ [ 0 , n ] , g i ∈ G . 条件:G是群,∀n∈N,i∈[0,n],g_i∈G. 条件:G是群,∀n∈N,i∈[0,n],gi∈G.
证明:
( g 0 g 1 ⋅ ⋅ ⋅ g n ) ∗ ( ( g n ) − 1 ( g n − 1 ) − 1 ⋅ ⋅ ⋅ ( g 0 ) − 1 ) (g_0g_1···g_n)*((g_n)^{-1}(g_{n-1})^{-1}···(g_0)^{-1}) (g0g1⋅⋅⋅gn)∗((gn)−1(gn−1)−1⋅⋅⋅(g0)−1)
根据结合律有
= g 0 g 1 ⋅ ⋅ ⋅ [ ( g n ∗ ( g n ) − 1 ] ( g n − 1 ) − 1 ⋅ ⋅ ⋅ ( g 0 ) − 1 =g_0g_1···[(g_n*(g_n)^{-1}](g_{n-1})^{-1}···(g_0)^{-1} =g0g1⋅⋅⋅[(gn∗(gn)−1](gn−1)−1⋅⋅⋅(g0)−1
= g 0 g 1 ⋅ ⋅ ⋅ [ g n − 1 ( g n − 1 ) − 1 ] ⋅ ⋅ ⋅ ( g 0 ) − 1 =g_0g_1···[g_{n-1}(g_{n-1})^{-1}]···(g_0)^{-1} =g0g1⋅⋅⋅[gn−1(gn−1)−1]⋅⋅⋅(g0)−1
= ⋅ ⋅ ⋅ =··· =⋅⋅⋅
= e =e =e
故 g 0 g 1 ⋅ ⋅ ⋅ g n 的 逆 元 是 ( g n ) − 1 ( g n − 1 ) − 1 ⋅ ⋅ ⋅ ( g 0 ) − 1 故g_0g_1···g_n的逆元是(g_n)^{-1}(g_{n-1})^{-1}···(g_0)^{-1} 故g0g1⋅⋅⋅gn的逆元是(gn)−1(gn−1)−1⋅⋅⋅(g0)−1