基本概念

1.环

1.1.环的定义

1.2.环的性质

基本概念：

• 两种单位元和两种逆元：
  

• 基本性质：
  

1.3.几种特殊的环

• 交换环：如果一个环的乘法运算是可交换的，那么就称这个环是交换环。
• 含幺环：如果一个环的乘法运算含有幺元，那么就称这个环是含幺环。
• 无零因子环和零因子：如果对于环中的任意两个元素，如果这两个元素都不是加法幺元，那么两个元素的乘法运算结果一定不等于加法幺元。则称这个环是无零因子环。如果两个元素的乘法运算结果是加法幺元，那么这两个元素就分别称为该环的左零因子和右零因子。如果一个元素既是左零因子和右零因子，那么这个元素就是该环的零因子。
• 整环：如果一个环同时是交换环、含幺环和无零因子环，那么这个环就是一个整环。

无零因子与乘法消去律的等价性：在一个整环中，无零因子条件等价于乘法消去律。

1.4.子环

子环的定义：如果一个环的集合的非空子集也构成环，那么这个环就称为原先的环的子环；如果一个环的集合的子集是真子集，那么这个环就称为原先的环的真子环。

子环判定定理：

2.域

2.1.域的定义

域的定义：

域与环的关系：

• 域一定是整环。
• 有限整环一定是域。

2.2.环与域的同态

环到环的同态映射：

环的同态像定理：任何环的同态像都是环。

相关题型

1.验证一个代数系统是否是一个环

基本思路：验证一个代数系统是否是一个环，只需要分别判定如下几点：

• 验证加法代数系统是否是一个阿贝尔群。也就是说首先需要验证代数系统满足封闭性与可结合性、存在幺元、每个元素存在逆元且运算可交换五个条件。
• 验证乘法代数系统是否是一个半群。也就是说要需要验证代数系统是否满足封闭性和可结合性这两个条件。
• 验证加法对乘法运算是否满足可分配性：需要分别验证是否满足左可分配性和右可分配性。

例题1：

解析：
首先验证加法代数系统是否是一个阿贝尔群。可以判断加法运算满足封闭性（任意两个函数相加的结果仍然是一个函数）、可结合性（多个函数相加的顺序不影响相加结果）、存在幺元（取值恒为0的函数）、每个元素存在逆元（与自身取值相反的函数），同时运算满足可交换群。由此可以判断该群是一个阿贝尔群。
接着验证乘法代数系统是一个半群。可以通过类似的方法判断乘法运算满足封闭性和可结合性。
最后验证该代数系统是否满足分配律。验证过程如下：

例题2：

解析：过程与上一题类似，在此不再赘述。

例题3：

解析：

例题4：

2.判断一个代数系统是否是整环

例题1：

3.判断一个代数系统是否是另一个代数系统的子环

例题1：

4.判断一个代数系统是否是域

例题1：

例题2：

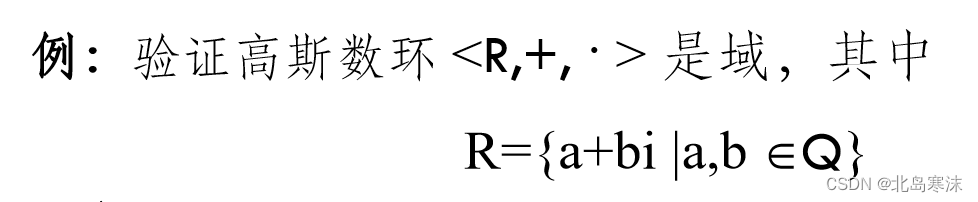
解析：

例题3：

解析：