矩阵运算
什么是矩阵
矩阵就是一组排列起来的向量,其中向量的维数(特征数)是矩阵的行,向量的个数是矩阵的列。
例如一个 n × m n \times m n×m的矩阵,代表着有 m m m个具有 n n n维特征的向量:
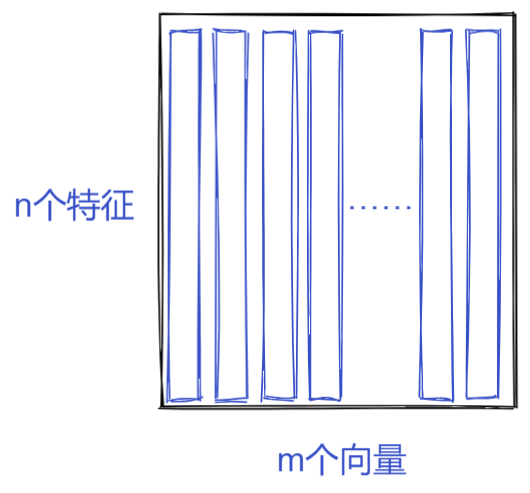
- 这是一个 2 × 3 2\times3 2×3的矩阵,表示由3个具有2个特征的向量组成:
x = [ a 11 a 12 a 13 a 21 a 22 a 23 ] x=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} x=[a11a21a12a22a13a23]
理解矩阵和向量的运算
首先,我们看一个方阵和一个向量的运算:
w = M × v = [ m 11 m 12 m 21 m 22 ] × [ v 1 v 2 ] = [ v 1 m 11 + v 2 m 12 v 2 m 21 + v 2 m 22 ] w=M\times v=\begin{bmatrix} m_{11} & m_{12}\\ m_{21} & m_{22}\\ \end{bmatrix} \times \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} =\begin{bmatrix} v_1 m_{11}+ v_2m_{12}\\ v_2m_{21}+ v_2 m_{22}\end{bmatrix} w=M×v=[m11m21m12m22]×[v1v2]=[v1m11+v2m12v2m21+v2m22]
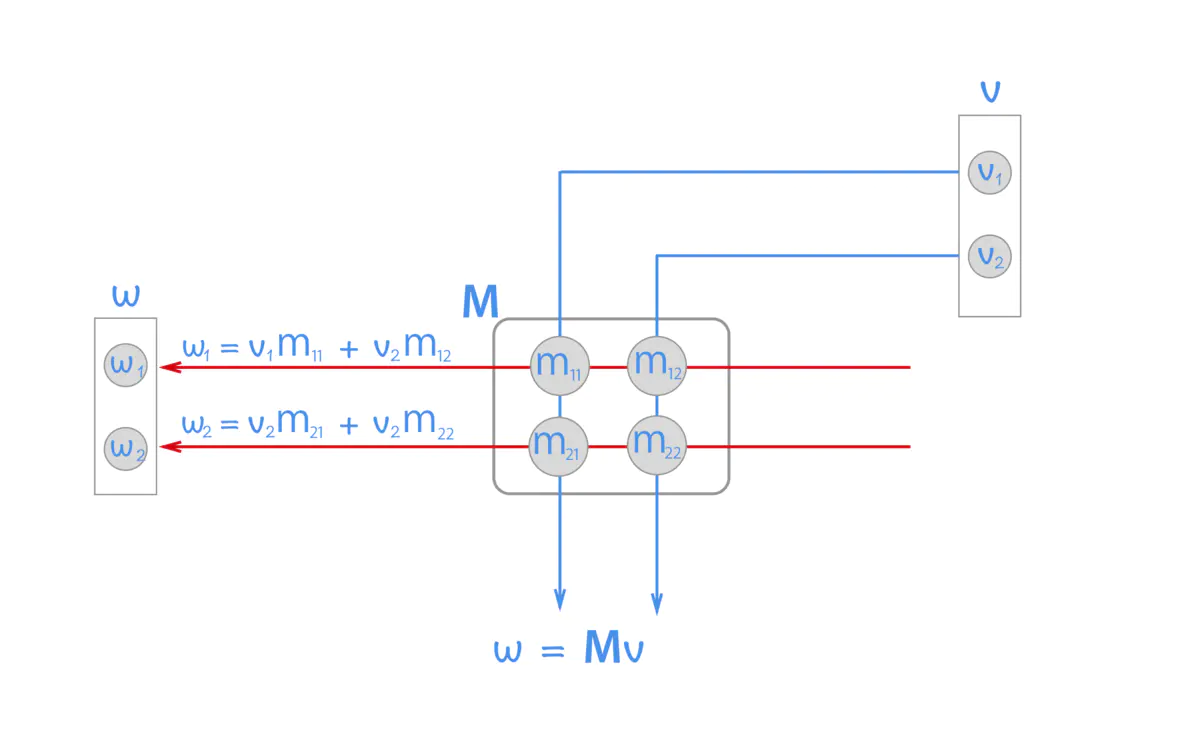
直观来看,可以先把向量 v v v向左倾倒,然后一次和矩阵 M M M中的每一行的对应元素相乘并相加每向下处理过一层,就产生一个新的结果。因此,最终相乘的结果,还是一个向量。这个向量的特征数等于矩阵 M M M的行数(特征数),向量的个数等于向量 v v v的个数。
为什么要把向量和矩阵相乘呢?直接把答案说出来,就是为了变换向量所在的空间。
矩阵运算的本质:向量的空间变换(线性变换)
在一个二维平面里,我们一般默认其基向量 e x = ( 1 , 0 ) , e y = ( 0 , 1 ) e_x=(1,0),e_y=(0,1) ex=(1,0),ey=(0,1),比如我们选取其中的一个向量 w = 5 e x + 2 e y w=5e_x+2e_y w=5ex+2ey。
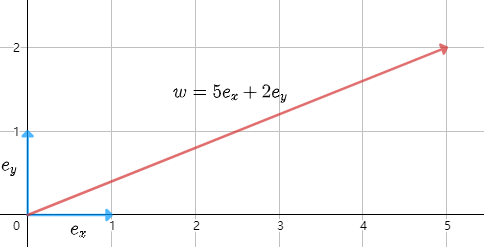

现在,我们要换一组基向量表示这个二维空间,在更换的过程里,我们要让一些条件保持不变:
- 原点位置不变;
- 平行线变换后仍旧是平行线;
- 直线变换后仍旧是直线;
以上的变换条件就是线性变换。可以想象成把空间坐标进行了几何上的扭曲。
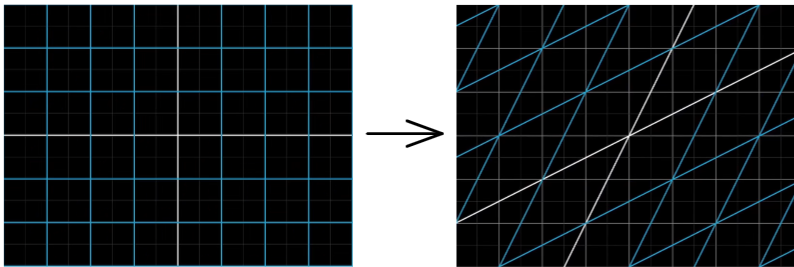
任何一个空间中的向量都可以通过基向量的运算得到,比如一个向量 v = − 1 e x + 2 e y v=-1e_x+2e_y v=−1ex+2ey。
当我们对空间进行了变换之后, v = − 1 e ^ x + 2 e ^ y v=-1{\hat e}_x+2{\hat e}_y v=−1e^x+2e^y。
e x = ( 1 , 0 ) , e y = ( 0 , 1 ) e_x=(1,0),e_y=(0,1) ex=(1,0),ey=(0,1)
e ^ x = ( 1 , − 2 ) , e ^ y = ( 3 , 0 ) {\hat e}_x=(1,-2),{\hat e}_y=(3,0) e^x=(1,−2),e^y=(3,0)
v ^ = − 1 e ^ x + 2 e ^ y = − 1 ( 1 , − 2 ) + 2 ( 3 , 0 ) = ( 5 , 2 ) {\hat v}=-1{\hat e}_x+2{\hat e}_y=-1(1,-2)+2(3,0)=(5,2) v^=−1e^x+2e^y=−1(1,−2)+2(3,0)=(5,2)
我们现在用纵向的矩阵来表示向量:
v = − 1 [ 1 0 ] + 2 [ 0 1 ] = [ − 1 2 ] v = -1\begin{bmatrix} 1\\0\end{bmatrix} +2\begin{bmatrix} 0\\1\end{bmatrix} =\begin{bmatrix} -1\\2\end{bmatrix} v=−1[10]+2[01]=[−12]
v ^ = − 1 [ 1 − 2 ] + 2 [ 3 0 ] = [ 5 2 ] {\hat v} = -1\begin{bmatrix} 1\\-2\end{bmatrix} +2\begin{bmatrix} 3\\0\end{bmatrix} =\begin{bmatrix} 5\\2\end{bmatrix} v^=−1[1−2]+2[30]=[52]
一般的,我们将变换后的基向量用一个矩阵表示:
[ 3 2 − 2 1 ] \begin{bmatrix} 3 & 2\\-2 & 1\end{bmatrix} [3−221]
更一般的,我们用字母表示:
[ a b c d ] \begin{bmatrix} a & b\\c & d\end{bmatrix} [acbd]
我们把第一列 [ a c ] \begin{bmatrix} a \\c\end{bmatrix} [ac] 看作第一个基准向量的落脚点,第二列 [ b b ] \begin{bmatrix} b \\b\end{bmatrix} [bb] 看作第二个基准向量的落脚点。如果把这个变换作用于向量 [ x y ] \begin{bmatrix} x \\y\end{bmatrix} [xy] ,就会得到 [ a x + b y c x + d y ] \left[\begin{array}{l}a x+b y \\c x+d y\end{array}\right] [ax+bycx+dy]。
进一步,我们把它定义为矩阵乘法:
[ a b c d ] [ x y ] = x [ a c ] + y [ b d ] = [ a x + b y c x + d y ] {\color{Red}\left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]=x\left[\begin{array}{l}a \\c\end{array}\right]+y\left[\begin{array}{l}b \\d\end{array}\right]=\left[\begin{array}{l}a x+b y \\c x+d y\end{array}\right]} [acbd][xy]=x[ac]+y[bd]=[ax+bycx+dy]
矩阵乘法
以上我们所说的是用一个矩阵表示一个向量在二维空间中的一次线性变换,如果我们要进行多次变换,也就是复合变换,应该怎么做?
我们就需要先进行了一次变换,得到变换后的向量,在进行同样的变换。但是最终结果,应该和复合矩阵对向量变换后的结果相同。

我们不妨将这称为两个矩阵的积。
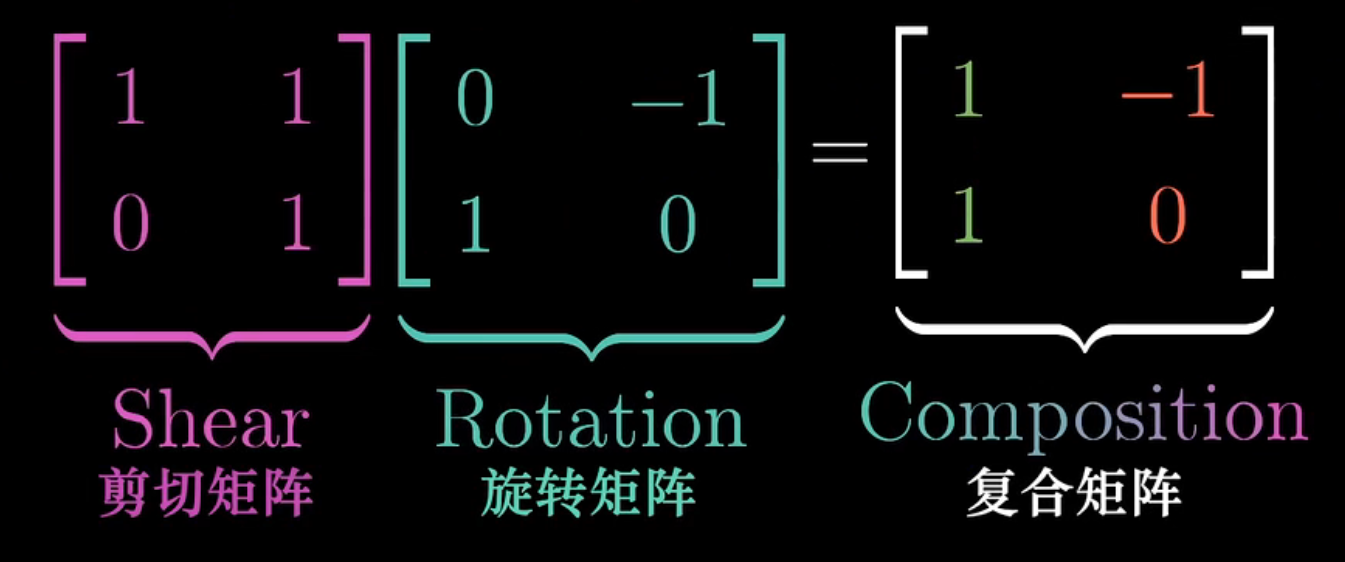
如何理解?可以理解为先作用右边的矩阵,再作用左边的矩阵。
对于一个一般的矩阵乘法:
[ a b c d ] [ e f g h ] \left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{ll}e & f \\g & h\end{array}\right] [acbd][egfh]
我们可以先认为基准 e x e_x ex先落到了 [ e g ] \begin{bmatrix} e \\g\end{bmatrix} [eg] , [ e g ] \begin{bmatrix} e \\g\end{bmatrix} [eg] 再经过变换落到:
[ a b c d ] [ e g ] = [ a e + b g c e + d g ] \left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{ll}e \\g\end{array}\right]=\left[\begin{array}{ll}ae+bg\\ce+dg\end{array}\right] [acbd][eg]=[ae+bgce+dg]
同样的基准 e y e_y ey经过两次变换:
[ a b c d ] [ f h ] = [ a f + b h c f + d h ] \left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{ll}f \\h\end{array}\right]=\left[\begin{array}{ll}af+bh\\cf+dh\end{array}\right] [acbd][fh]=[af+bhcf+dh]
最终,这个矩阵乘法变换成了:
[ a b c d ] [ e f g h ] = [ a e + b g a f + b h c e + d g c f + d h ] {\color{Red}\left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{ll}e & f \\g & h\end{array}\right]=\left[\begin{array}{ll}a e+b g & a f+b h \\c e+d g & c f+d h\end{array}\right]} [acbd][egfh]=[ae+bgce+dgaf+bhcf+dh]