1. 什么是决策树？

决策树是最早的机器学习算法之一，起源于对人类某些决策过程 的模仿，属于监督学习算法。

决策树的优点是易于理解，有些决策树既可以做分类，也可以做回归。在排名前十的数据挖掘算法中有两种是决策树[1]。决策树有许多不同版本，典型版本是最早出现的ID3算法，以及对其改进后形成的C4.5算法，这两种算法可用于分类。对ID3算法改进的另一个分支为“分类和回归树”（Classification AndRegression Trees，CART）算法，可用于分类或回归。CART算法为随机森林和Boosting等重要算法提供了基础。在OpenCV中，决策树实现的是CART算法。

2.决策树原理

2.1 决策树的基本思想

最早的决策树是利用if-then结构来分割数据的，其中，if表示条
件，then就是选择或决策。

2.2 决策树的表示方法

在决策树中，通常将样本向量中的特征称为样本的属性，下文将
使用“属性”这一习惯性称呼。

决策树通过把样本从根节点排列到某个叶子节点对样本进行分类。 根节点是树第一次切分的位置，叶子节点即为样本所属的分类标签。
树上的每一个节点都表示了对样本的某个属性的测试，并且该节点的每一个后继分支对应于该属性的一个可能值。分类样本的方法是从这棵树的根节点开始，测试这个节点指定的属性，然后按照给定样本的该属性值对应的树枝向下移动。这一过程在以新节点为根的子树上重复。

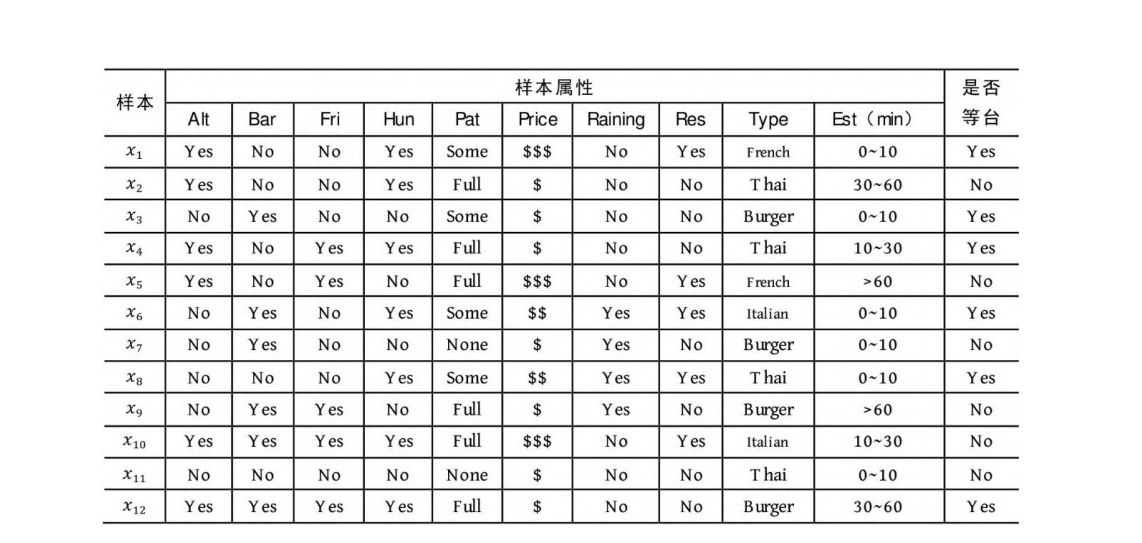
下面用顾客在271餐厅就餐时的等台意愿示例说明决策树[1]。表5-
1为数据集样本的属性列表，表5-2为数据集，在数据集中共12个样
本，每个样本有10个属性，样本的标签为是否愿意等台，因此这是一个二分类问题。从已有的数据集推断出的决策树的结构如图5-1所示。

表5-2 餐厅等台意愿数据集

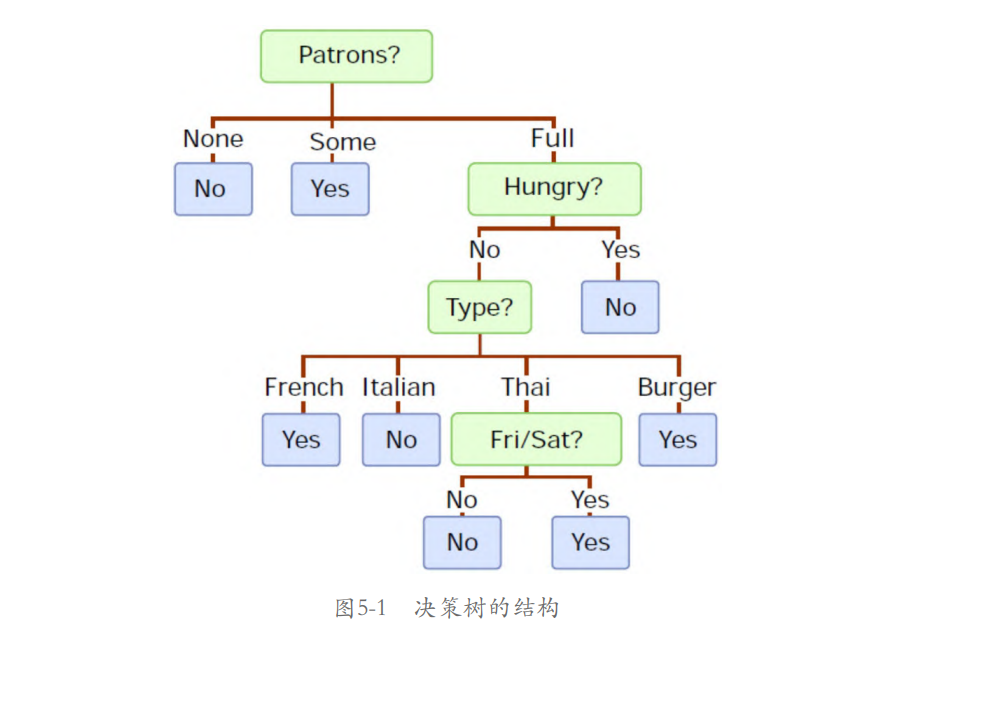
如图5-1所示，方框中带有问号的为根节点（按给定的属性切分数
据），其余为叶子节点（标签）。

开始时决策树根据餐厅用餐人数多少（Patrons属性）将数据集切分为3个子集，左子集为无人用餐，中间子集为有一些人用餐，右子集为客满。其他子树的根节点原理与之类似。

当有新的未知数据出现时，即可根据特征简单地遍历树并到达确定标签，即是否愿意等台。尽管例子很简单，但它清楚地体现了决策树模型的可解释性，以及学习简单规则的能力。

扫描二维码关注公众号，回复： 16347259 查看本文章

从示例可知，决策树的核心问题是：自顶向下的各个节点应选择
何种属性进行切分，才能获得最好的分类器？因此，选择最佳切分属性是决策树的关键所在。

2.3 最佳切分属性的选择

评 价 最 佳 切 分 属 性 通 常 是 基 于 样 本 不 纯 度 减 少 （ImpurityReduction）或者纯度增益（Purity Gain）这一思想的。样本纯度指的是集合中样本类型的同质性（Homogeneity），如果数据集中只有一种类型的样本，则该数据集的样本纯度最高，不纯度最低。数据集中样本类型越多，则样本纯度越低，不纯度越高。显然，我们希望样本集按某属性切分后，其样本纯度提高，不纯度降低，即切分后样本集的纯度增益越大越好。

为 了 计 算 纯 度 增 益 ， 需 要 定 义 不 纯 度 测 度 （ Impurity
Measure），即计算不纯度的方法；然后用节点切分前的不纯度减去切分后的不纯度，得到不纯度减少（即纯度增益）的指标；最后选择使不纯度减少最多的属性进行切分。

不同种类的决策树采用不同的方式测量样本的不纯度，例如信息熵、基尼系数、圴方误差等。下面介绍几种常用的计算不纯度和选择最优切分属性的方法。

1. 信息熵
ID3算法使用信息增益（Information Gain）选择最佳属性构建决策树，即使用能获得最大信息增益的属性作为划分当前数据集的最佳属性。想要了解信息增益的计算方法，首先需要了解其概念。

信息熵（Information Entropy）是美国信息学家香农于1948年提
出的。信息是对不确定性的消除，而不确定性可以用概率来度量。某事件出现的概率越高，其不确定性就越低，反之，不确定性就越高。信息熵是消除不确定性所需信息量的度量，即未知事件可能含有的信息量。事件出现的概率越低，不确定性越大，则信息量越大，熵越大；概率越高，不确定性越小，则信息量越小，熵越小。

下面从信息论的角度介绍信息熵与信息增益[1]。定义不确定性函
数I表示事件的信息量，它与事件发生的概率p应满足以下条件：

◎ I§≥0, I(1)=0，即任何事件的信息量都是非负的，概率为1
的事件的信息量为0。

◎I(p1∙p2)=I(p1)+I(p2)，即两个独立事件所产生的信息量应等于
各自信息量之和。

◎ I§连续，且为概率p的单调递减函数，概率的微小变化对应
于信息量的微小变化。

人们发现，对数函数同时满足上述条件，因此，可使用式（5-1）
表示事件的信息量：

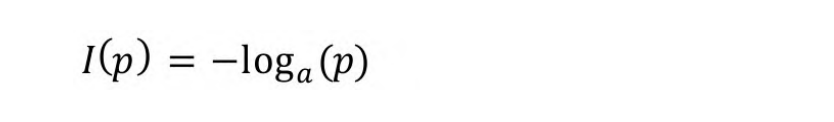
式中，若取a=2，就是常说的信息单位bit（比特）。例如，抛一枚正常硬币出现正面的事件给出的信息量为−log2(0.5)=1bit。如果对于一枚铸造时有偏差的硬币，且出现正面的概率为0.99，则抛此硬币出现正面的事件给出的信息量为

−log2(0.99)=0.0145bit。

如果有多个事件，那么这些事件的平均信息量应如何计算呢？

假设事件v1, …, vJ发生的概率为p1, …, pJ，其中，[p1, …, pJ]为离
散概率分布。则多个事件的平均信息量用式（5-2）定义：

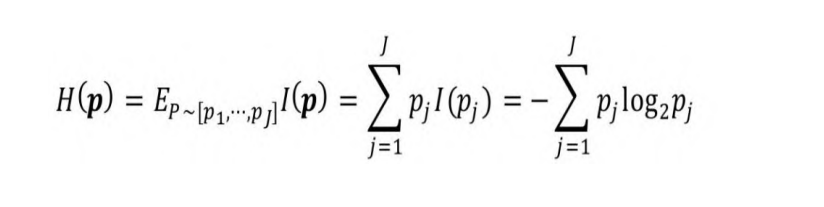
式中，H§为离散分布p的信息熵，p=[p1, …, pJ]。在有关熵的所有
计算中，定义0lg0=0。如果事件仅有两种类型（布尔型），则概率为
p=[p1, 1−p1]。

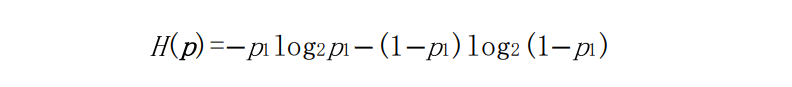
假设D是一个有14个样本的布尔型集合，包括9个正样本，5个负样
本。根据式（5-2）计算D的信息熵如下：

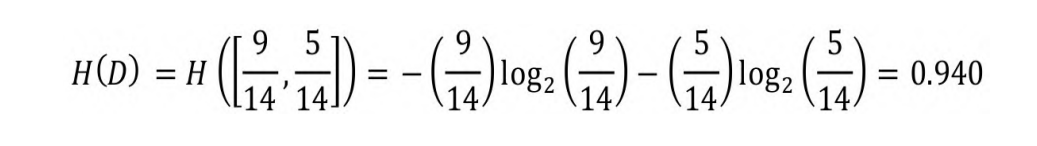
如果D的所有成员都属于同一类，即H(D)=H([1, 0])，则D的信息
熵H(D)→0。如果D中正负样本的出现概率均为0.5，则H(D)=H([0.5,
0.5])=1。由此可见，在布尔型集合中，当正负样本的出现概率相等时信息熵最大。

信息熵是事物不确定性的度量标准，在决策树中，它不仅能用来
度量类别的不确定性，还可以用来度量包含不同特征的数据样本的不确定性。某个特征列向量的信息熵越大，说明该特征的不确定性越大，即混乱程度越大，因而应优先考虑从该特征着手进行切分。信息熵为决策树的切分提供了最重要的依据和标准。

2. 信息增益

属性A对训练数据集D的信息增益为G(D, A)，即集合D的信息熵
H(D)与属性A给定的条件下D的条件熵H(D|A)之差：

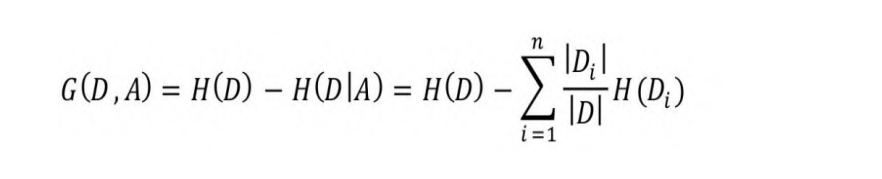
式中，n表示针对属性A，样本集合被切分为n个子集（即属性A的n种取值）；|Di|表示按属性A切分后的第i个子集的样本数量，|D|表示样本集合D的样本数量。

H(D)度量了D的不确定性，条件熵H(D|A)度量了在知道属性A以后D
剩下的不确定性，由此可知，H(D)−H(D|A)就度量了D在知道属性A以后不确定性的减少程度。这个度量在信息论中称为互信息，在决策树ID3算法中称为信息增益。

回到前文介绍的餐厅示例，原始数据集D包含[x1, …, x12]共12个
样本，每个样本的特征向量有10个属性，标签为是否会等台，其中，
[x1, x3, x4, x6, x8, x12]6人决定等台，[x2x5, x7, x9, x110, x11]6人
决定不等台。如图5-2（a）所示，按Patrons属性可以切分为None、Some和Full共3个子集，即n=3（Patrons属性的3种取值）。按Patrons属性切分的信息增益如下：

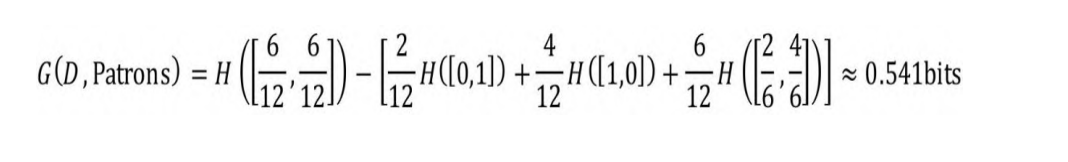
如图5-2（b）所示，按Type属性可以分为French、Italian、Thai
和Burger共4个子集，即n=4（Type属性的4种取值）。按Type属性切分的信息增益如下：

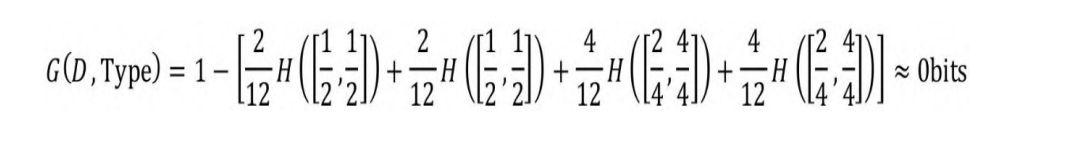
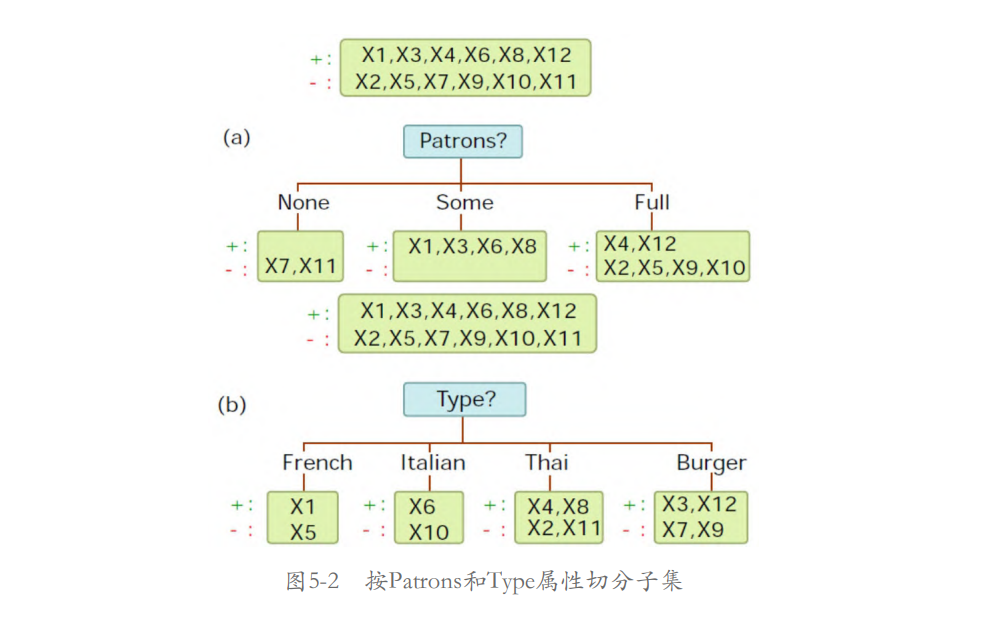
显然G(D, Patrons) > G(D, Type)。事实上，按Patrons属性切分
的信息增益是最高的。因此，选择Patrons属性作为根节点的属性开始切分。

3. 信息增益率

ID3算法采用信息增益的方式存在诸多问题。例如，在相同条件下，取值较多的属性（n较大）比取值较少的属性的信息增益要大，即信息增益作为标准容易偏向于取值较多的特征。比如，一个属性有2个取值，概率各为1/2；另一个属性有3个取值，概率各为1/3。其实它们都是完全不确定的变量，但是取3个值的比取2个值的信息增益要大。

C4.5算法对此进行了改进，它使用信息增益率（Information
Gain Ratio）作为切分准则。信息增益率是信息增益与特征熵的比
值：

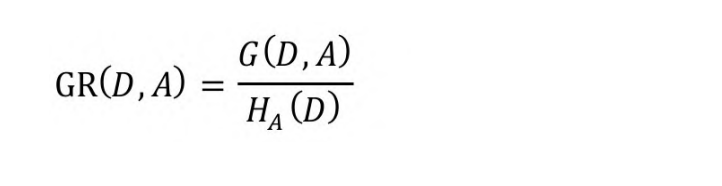
式中，D为样本集合，A为样本属性，属性A的特征熵HA(D)的表达式如下：

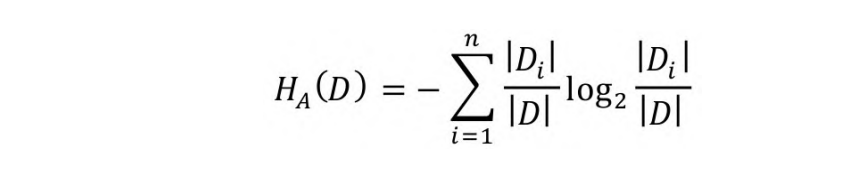
根据上式，示例中Patrons属性的特征熵为：

也就是说，当通过信息增益率选择最优切分属性时，Patrons属性
和Type属性相比，应选择Patrons属性。

4. 基尼系数

无论ID3算法还是C4.5算法，都是基于信息熵模型的，涉及大量对
数运算。为了简化运算，同时保留信息熵模型的优点，CART算法提出了使用基尼系数来代替信息增益率。基尼系数（Gini Index）代表了模型的不纯度，基尼系数越小，模型的不纯度越低，对应的属性越好。

具体而言，在分类问题中，假设样本共有J个类别，第j类的概率
为pj，则基尼系数的表达式为：

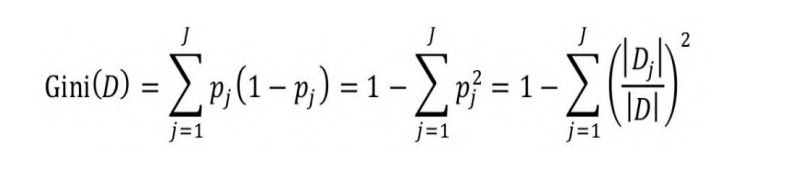
式中，|Dj|为第j类样本的数量，|D|为样本集D的样本数量。

如果是二分类问题，若样本属于第一类的概率是p，则基尼系数的
表达式为：

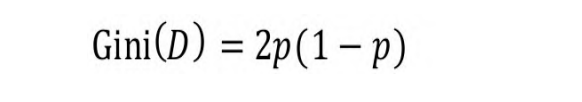
如果根据属性A把D分成n个部分，则在属性A的条件下，D的基尼系
数的表达式为：

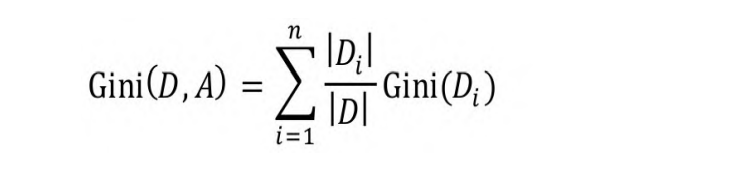
基尼系数最小的那个属性进行切分。

二分类节点不纯度与某一类样本出现概率p的关系曲线如图5-3所示，为了便于比较，将信息熵缩小了两倍，使其与基尼系数曲线都通过(0.5, 0.5)点。

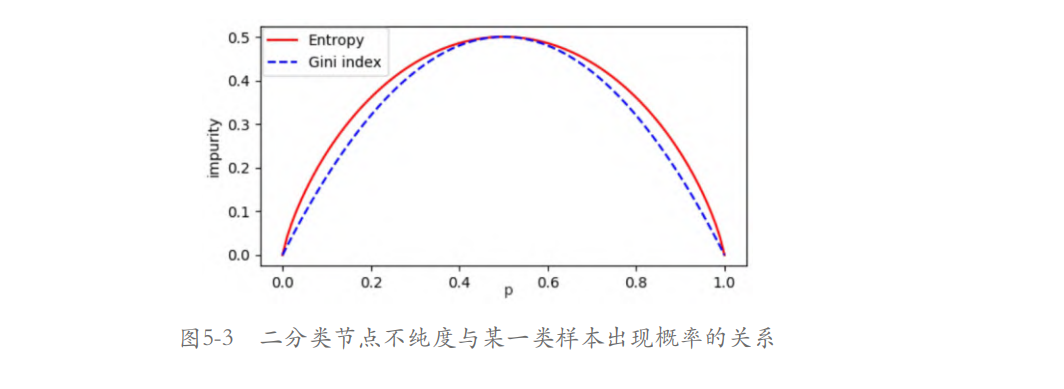
从图5-3可以看出，基尼系数和信息熵的曲线非常接近。因此，基
尼系数可以作为熵模型的一个近似替代。而CART算法就是使用基尼系数来选择决策树的特征的。同时，为了进一步简化，CART算法每次仅仅对某个特征的值进行二分，这样CART算法建立起来的就是二叉树，进一步简化了计算。

5. 均方误差

前文介绍的都是分类树的计算方法，输出的是离散的类别，例如
在餐厅等台或者不等台等。而回归树输出的是连续的数值，如预测房价等。为了实现回归树，需要使用适合回归的不纯度测度。均方误差（Mean Squared Error，MSE）主要用于回归树，为观测值与预测值之差的平方。

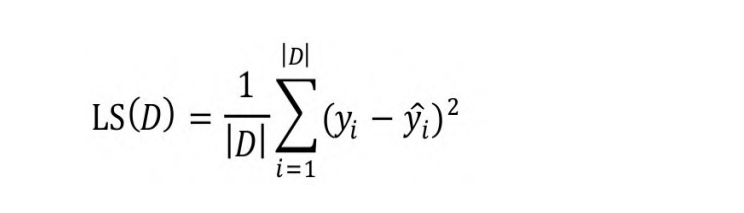
式中，|D|是数据集D的样本数量，yi和 分别为第i个样本的输出值和
预测值。可以用输出值yi的平均值来代替预测值：

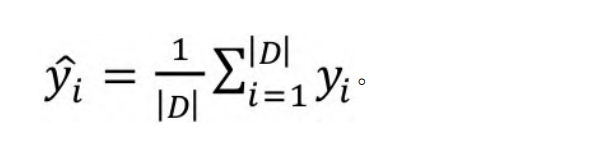
如果根据属性A将集合D切分为n个子集，则切分后的均方误差为：

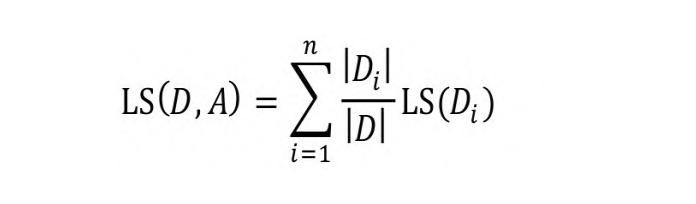
CART回归模型使用了均方误差的度量方式，其目标是对于任意切
分属性A对应的任意节点S两边划分成的数据集D1和D2，求出使数据集D1和D2各自的均方差最小，同时，D1和D2的均方差之和最小所对应的属性，表达式为：

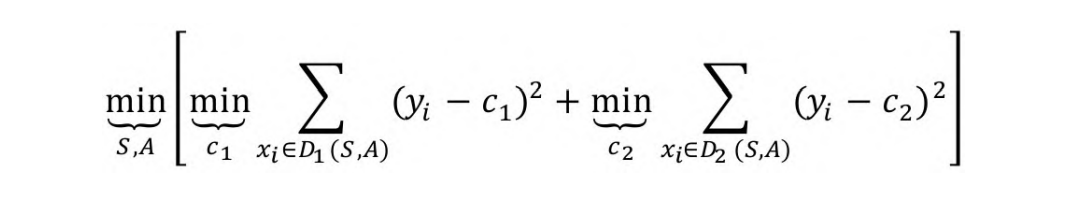
其中，c1为D1数据集的样本输出均值，c2为D2数据集的样本输出均值。

CART分类树采用叶子节点中概率最大的类别作为当前节点的预测
类别。回归树输出的不是类别，它采用的是用最终叶子的均值或者中位数来预测输出结果。

停止标准

如前文所述，决策树遵循贪婪的递归分裂节点，它们是如何停止
又是何时停止的呢？

实际上，可以应用许多策略来定义停止标准（Stopping Criteria）。最常见的是数据点的最小数量，如果进一步切分会违反此约束，则停止切分。
另一个停止标准是树的深度。停止标准与其他参数一起可以帮助我们实现具有较好泛化能力的决策树模型。非常深或具有太多非叶子节点的决策树通常会导致过拟合。

剪枝

由于决策树的建立完全依赖训练样本，因此算法很容易对训练集
过拟合，导致泛化能力变差。为了解决过拟合问题，需要对决策树进行剪枝（Pruning），即去掉一些节点，包括叶子节点和中间节点，以简化决策树。剪枝类似于线性回归的正则化，可以增加决策树的泛化能力。

剪枝的常用方法有预剪枝和后剪枝两种。

预剪枝是在构建决策树过程中，提前终止决策树的生长，从而避免产生过多节点。该方法简单，但实用性不强，因为很难准确判断应何时终止生长。

后剪枝是在决策树构建完成后再去掉一些节点。常见的后剪枝方法有悲观错误剪枝、最小错误剪枝、代价复杂度剪枝和基于错误的剪枝四种。OpenCV中的CART算法采用的是代价复杂度剪枝，即先生成决策树，然后生成所有可能的剪枝后的CART树，最后使用交叉验证来检验各种剪枝的效果，选择泛化能力最好的剪枝策略。