常用命令

命令	功能
format long	定义输出格式为长格式(15 位数字)
xi = linspace(1,2,100)	构造 100 个元素的数组，其值从 1 到 2 均匀分布
xi.^2	群运算，对向量 xi 中所有元素进行幂运算
plot(xi,yi,x,y,’o’,x0,y0,’*’)	画图，其中 xi,yi 是向量，画出一条曲线，(x,y) 画’o’，(x0,y0) 画 ‘*’
A’	矩阵 A 的转置
[A,B] = meshgrid(x,y)	用于从数组 x 和 y 产生网格，生成 size(y)*size(x) 大小的矩阵 A 和 B。它相当于 x 从一行重复增加到 size(y) 行，把 y 转置成一列再重复增加到 size(x) 列
c = regress(y,x)	y 是因变量数据向量，x 是自变量数据矩阵。输出向量 c 为回归系数估计值

例1. 求解线性代数

从一桶（31.5 加仑）原油中，不同的炼油厂可生成石油产品如下（单位：加仑）

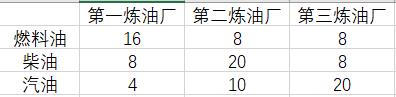
（1）现在需要 9600 加仑燃料油，12800 加仑柴油及 16000 加仑汽油，则每个炼油厂所用石油的桶数是多少？
（2）假设上述的炼油厂模型中汽油的生产无关紧要（储油罐里有充分的储存量），我们只关心燃料油与柴油的需求，则每个炼油厂所用的石油桶数各是多少？
（3）假定炼油厂模型中的第二个炼油厂停产，而我们必须设法由仅有的两个炼油厂满足需求，则这两个炼油厂所用的石油桶数各是多少？

---

（1）设 $x_i$( $i$ = 1,2,3)，表示第 $i$ 个炼油厂所用石油的桶数
则 $x_i$ 满足
$$\begin{cases} 16x_1 + 8x_2 + 8x_3 = 9600\\ 8x_1 + 20x_2 + 8x_3 = 12800\\ 4x_1 + 10x_2 + 20x_3 = 16000\\ \end{cases}$$
令 A = $\begin{bmatrix} 16 & 8 & 8 \\ 8 & 20 & 8 \\ 4 & 10 & 20 \end{bmatrix}$， $x$ = $\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$，b = $\begin{bmatrix} 9600 \\ 12800 \\ 16000 \end{bmatrix}$，则解方程组 A $x$ = b 可得每个炼油厂所用石油的桶数

x1 = [16;8;4];
x2 = [8;20;10];
x3 = [8;8;20];
A = [x1 x2 x3];
b = [9600;12800;16000];
x = inv(A)*b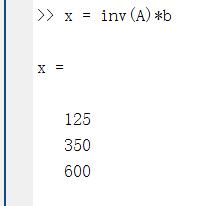

即三个炼油厂分别用 125、350 和 600 桶石油

（2）由于不考虑汽油的生产量，因此方程组变为

$$\begin{cases} 16x_1 + 8x_2 + 8x_3 = 9600\\ 8x_1 + 20x_2 + 8x_3 = 12800\\ \end{cases}$$
令 B = $\begin{bmatrix} 16 & 8 & 8 \\ 8 & 20 & 8 \\ \end{bmatrix}$， $y$ = $\begin{bmatrix} y_1 \\ y_2 \\ \end{bmatrix}$， $d$ = $\begin{bmatrix} 9600 \\ 12800 \\ \end{bmatrix}$，因此经初等变换可将 B 化为行最简形 B $_0$，由此可得石油桶数

B = [16 8 8;8 20 8];
d = [9600;12800];
[B0,i] = rref([B,d])

由运行结果可以看出，

$$\begin{cases} x_1 = 350 - 0.3750*x _3\\ x_2 = 500 - 0.2500*x _3\\ \end{cases}$$

（3）由于第二炼油厂停产，因此方程组变为

$$\begin{cases} 16x_1 + 8x_3 = 9600\\ 8x_1 + 8x_3 = 12800\\ 4x_1 + 20x_3 = 16000\\ \end{cases}$$

A = [16 8;8 8;4 20];
b = [9600;12800;16000];
x = inv(A'*A)*A'*b;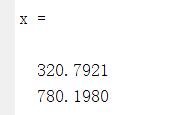

此时第一和第三炼油厂需要的石油至少是 320 和 780 桶

例2. 三次多项式插值

用三次多项式插值公式计算 $f(1.1300)$ 的近似值，并作出图形

根据已知条件，把 4 个点的做标识 $x_1$ = 1.1275, $x_2$ = 1.1503, $x_3$ = 1.1735,$x_4$ = 1.1973 分别代入三次多项式 $p(x)$ = $a_0$ + $a_1x$ + $a_2x^2$ + $a_3x^3$ 中，可得：

$$\begin{cases} a_0 + 1.1275a_1 + 1.1275^2a_2 + 1.1275^3a_3 = 0.1191\\ a_0 + 1.1503a_1 + 1.1503^2a_2 + 1.1503^3a_3 = 0.13954\\ a_0 + 1.1735a_1 + 1.1735^2a_2 + 1.1735^3a_3 = 0.15932\\ a_0 + 1.1972a_1 + 1.1972^2a_2 + 1.1972^3a_3 = 0.17903\\ \end{cases}$$

format long   % 定义输出格式为长格式
A = [1 1.1275 1.1275^2 1.1275^3;    
     1 1.1503 1.1503^2 1.1503^3;
     1 1.1735 1.1735^2 1.1735^3;
     1 1.1972 1.1972^2 1.1972^3];    % 输入矩阵 A
b = [0.1191;0.13954;0.15932;0.17903];   % 输入系数 b
a = inv(A)*b;          % 计算多项式的系数 
x0 = 1.1300;           % 输入需要计算的点 
y0 = a(1)+a(2)*x0+a(3)*x0^2+a(4)*x0^3   % 计算该点的值
x = [1.1275;1.1503;1.1735;1.1972];      % 输入已知点
y = [0.1191;0.13954;0.15932;0.17903];   
xi = linspace(1.1,1.3,2000);       % 构造数值 xi，从 1.1 到 1.3，取 2000 个等距值
yi = a(1)+a(2)*xi+a(3)*xi.^2+a(4)*xi.^3;   % 计算 xi 对应的多项式 yi
plot(xi,yi,x,y,'o',x0,y0,'*');   % 画图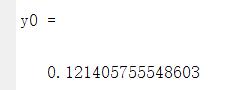

例3. 一元线性回归分析模型

根据下表预测 2011 年产量为 320 万件时的总成本

年度	产量 X（万件）	总成本 Y（万元）
2006	80	4600
2007	110	5500
2008	160	5850
2009	230	5350
2010	300	6200

假设成本 Y 是产量 X 的一次线性函数，即二者的关系是：Y = a + b*X

X = [80;110;160;230;300];
Y = [4600;5500;5850;5350;6200];
XX = [ones(5,1),X];  % 为了在回归得到常数项系数 a，将 XX 作为回归的自变量
C =regress(Y,XX)   % C 是一个回归系数矩阵

因此，可以认为产量与成本的关系为：Y = 4626.0 + 5.0 * X。
当 X = 320 万件时，Y = 6226（万元）