主成分分析、因子分析及其有关的数学基础

1、相关矩阵

2、单位矩阵

3、旋转

正余弦公式：

https://baike.baidu.com/item/%E4%B8%89%E8%A7%92%E5%87%BD%E6%95%B0%E5%85%AC%E5%BC%8F/4374733?fr=aladdin

旋转

翻译自: http://www.metro-hs.ac.jp/rs/sinohara/zahyou_rot/zahyou_rotate.htm
翻译：汤永康
出处: http://blog.csdn.NET/tangyongkang
转贴请注明出处
1 围绕原点的旋转
如下图，在2维坐标上，有一点p(x, y) , 直线opの长度为r, 直线op和x轴的正向的夹角为a。直线op围绕原点做逆时针方向b度的旋转，到达p’ (s,t)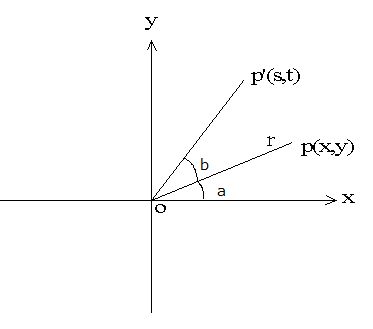

s = r cos(a + b) = r cos(a)cos(b) – r sin(a)sin(b)   (1.1)
t = r sin(a + b) = r sin(a)cos(b) + r cos(a) sin(b) (1.2)
其中 x = r cos(a) , y = r sin(a)
代入(1.1), (1.2) ,
s = x cos(b) – y sin(b)    (1.3)
t = x sin(b) + y cos(b)    (1.4)

用行列式表达如下：

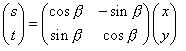
2．座标系的旋转
在原坐标系xoy中, 绕原点沿逆时针方向旋转theta度，变成座标系 sot。
设有某点p，在原坐标系中的坐标为 (x, y), 旋转后的新坐标为(s, t)。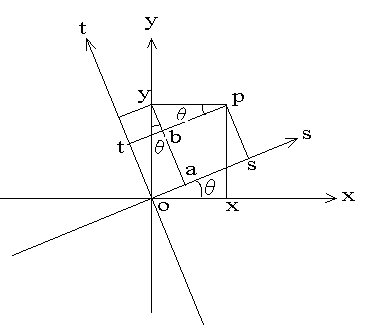

oa = y sin(theta) (2.1)
as = x cos(theta) (2.2)
综合(2.1)，(2.2) 2式
s = os = oa + as = x cos(theta) + y sin(theta)
t = ot = ay – ab = y cos(theta) – x sin(theta)

用行列式表达如下：

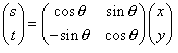
而您一旦用以下这图解方法，随时眼见显然，再也不会搞错。

原文地址：

http://blog.csdn.net/Tangyongkang/article/details/5484636

http://blog.sina.com.cn/s/blog_3fd642cf0101cc8w.html

4、特征值和特征向量：P行P列矩阵的特征值和特征向量，原则上讲，存在P组。

5、对称矩阵：关于主对角线对称

重要性质：

6、矩阵的加法，乘法，逆矩阵运算，转置矩阵运算

7、离差平方和、方差、标准差

离差平方和=（每个数据-平均值）^2相加之和

（总体）方差=离差平方和/数据个数

（总体）标准差=开平方总体方差

主成分分析

选出综合实力最强的一种分析方法：数据方差最大的地方画一条轴

注意点：

主成分 = a1u1 + a2u2 + ……apup a表示各个自变量对主成分的影响程度，u表示自变量的标准值
计算方法：分为非标准化分析和标准化分析，人们一般采用标准化分析
主成分个数：与自变量个数相同

cov(x,y)=E[(x-E(x))(y-E(y))]

Var(x)=E[(x-E(x))^2]

具体实例：

主成分分析流程：

求出主成分和主成分得分
确认分析结果的精度
讨论分析结果

步骤一：求出主成分和主成分得分

d <- data.frame(mian = c(2,1,5,2,3,4,4,1,3,5), peiliao = c(4,5,3,2,5,3,4,2,3,5), tang=c(5,1,4,3,5,2,3,1,2,3))
d <- data.frame(d,row.names=c('二乐','梦田屋','地回','菜之花','花之节','升轩','人藏拉面','海乐亭','鸣海家','奏乐'))
 #求出主成分和主成分得分
> #观察相关矩阵
> round(cor(d),2)
        mian peiliao tang
mian    1.00    0.19 0.36
peiliao 0.19    1.00 0.30
tang    0.36    0.30 1.00
> #可视化
> plot(d)
> #建立PCA
> prin <- prcomp(d,scale=TRUE)
> #检查主成分的旋转载荷
 print(prin)
Standard deviations (1, .., p=3):
[1] 1.2541347 0.9022241 0.7830312

Rotation (n x k) = (3 x 3):
              PC1        PC2        PC3
mian    0.5715110 -0.6044710  0.5549685
peiliao 0.5221161  0.7896069  0.3223595
tang    0.6330639 -0.1055260 -0.7668731
> #主成分的累积贡献度，各个主成分的重要度。
 summary(prin)
Importance of components:
                          PC1    PC2    PC3
Standard deviation     1.2541 0.9022 0.7830
Proportion of Variance 0.5243 0.2713 0.2044
Cumulative Proportion  0.5243 0.7956 1.0000
#查看结果
unclass(prin)
#绘制第一、第二主成分旋转载荷散点图
 plot(prin$rotation[,-3])
> text(prin$rotation[,-3],labels=colnames(d),adj=c(0,1))
#绘制主成分得分图
> plot(prin$x[,-3])
> text(prin$x[,-3],labels=rownames(d),pos=3)

步骤二：确认分析结果的精度

第i个主成分的贡献度 = 特征值/变数个数×100%

第i个主成分的贡献度说明：这个主成分汇集了多少分析对象的数据中所包含的信息

主成分分析成功与否通过累积贡献度的大小进行判断，希望第二主成分的累积贡献度达到50%以上

步骤三：讨论分析结果

通过步骤1的个体图和变量图讨论分析结果。

注意：

变量的选择和第1主成分的定义都需要分析者定义（进行分析详细说明为什么用这些变量进行分析），分析者要依据所要探求的‘综合xx实力’，收集相关变量。
累积贡献度的标准值
第二主成分及之后的主成分：
方差和特征向量:求出方差第i处大的轴同求出第i大特征值所对应的特征向量是一回事

因子分析

因子载荷量

潜在结构：公共因子

注意

因子分析的计算在于事先假定出公共因子的个数
因子个数：相关矩阵中比1大的特征值的个数
选择的分析视分析者的判断
因子计算通常需要对分析对象的数据逐一进行变量标准化
u1 = a11f1 + a12f2 + e1 a代表因子载荷量， u代表变量的标准值，f 代表公共因子，e 代表独立因子
u2 = a21f1 + a22f2 + e2
u3 = a31f1 + a32f2 + e3
确认因子载荷量的值：因子载荷量的值越大可以解释为这个公共因子对相应的因变量的影响也越大
在因子分析中因变量的选定是解决问题的关键，事先预定一定程度的结果。
因子分析是为确定‘因子载荷量’的值而确定的分析方法，分析之前已经知道大概隐藏着什么公共因子，因子载荷量的绝对值越大，我们可以解释为这个公共因子对相应的因变量的影响也就越大。

因子分析具体实例：

> data <- data.frame(dianmiansheji=c(5,5,4,2,3,5,5,3,4,1,3,4,3,4,1),  dianneiqifen=c(5,4,4,3,3,4,5,1,1,2,2,3,2,3,2),nvshengtaidu=c(5,5,4,4,3,5,5,2,3,2,3,4,3,4,3),hongcaiweidao=c(4,2,4,3,3,3,4,5,3,2,1,4,4,5,5),hongcaijiage=c(4,2,4,3,4,2,5,4,2,2,1,3,5,4,5),hongcakougan=c(2,2,4,3,1,3,5,4,3,2,1,4,5,5,4),row.names=LETTERS[1:15])
> cor(data)
> plot(data)
> prin <- prcomp(data,scale=TRUE)
> print(prin)
Standard deviations (1, .., p=6):
[1] 1.6332588 1.5384370 0.7250477 0.5098295 0.3587327 0.2266452

Rotation (n x k) = (6 x 6):
                     PC1        PC2         PC3        PC4        PC5
dianmiansheji -0.3998169  0.3719984  0.53607865  0.5650603  0.3032612
dianneiqifen  -0.4462135  0.3647448 -0.48701847 -0.1831161  0.0506540
nvshengtaidu  -0.4577695  0.4000234 -0.02670556 -0.3085370 -0.3542643
hongcaiweidao -0.3808422 -0.4677595  0.05130610  0.3415827 -0.6916304
hongcaijiage  -0.3803547 -0.4285156 -0.48910417  0.2532674  0.4842806
hongcakougan  -0.3765323 -0.4075967  0.48256014 -0.6092266  0.2590045
                      PC6
dianmiansheji -0.05588219
dianneiqifen  -0.62814839
nvshengtaidu   0.63954427
hongcaiweidao -0.19620539
hongcaijiage   0.36580011
hongcakougan  -0.14485726
> summary(prin)
Importance of components:
                          PC1    PC2     PC3     PC4     PC5     PC6
Standard deviation     1.6333 1.5384 0.72505 0.50983 0.35873 0.22665
Proportion of Variance 0.4446 0.3945 0.08762 0.04332 0.02145 0.00856
Cumulative Proportion  0.4446 0.8390 0.92667 0.96999 0.99144 1.00000
> plot(prin,type='line')
> biplot(prin)

假定:有2个公共因子：

因子分析流程：

求解旋转前的因子载荷量
求解旋转后的因子载荷量
解释各公共因子的含义
确认分析结果的精度
求出因子得分，充分理解每个个体的特征

步骤：求解旋转前的因子载荷量：找出公共因子所产生的影响程度

因子载荷量的计算方法有：主因子法，极大似然法等多种方法

> #变量标准化
> data.scale <- scale(data)
> #假定公共因子与独立因子，独立因子之间是不相关的。
> #还要假定公共因子之间不相关
> #假定公共因子平均值为0，方差为1.假定独立因子i平均值为0，方差为di.
> #任意两个公共因子之间的单相关系数的值为零，这种假定思想方法被称为正交因子模型，不作这种假定的思考方法称为斜交因子模型
> #正交因子模型
fac <- factanal(data.scale,factors=2,scores="regression",rotation='varimax')

Call:
factanal(x = data.scale, factors = 2，rotation='varimax')

Uniquenesses:  ##独立因子
dianmiansheji  dianneiqifen  nvshengtaidu hongcaiweidao  hongcaijiage 
        0.403         0.207         0.005         0.012         0.313 
 hongcakougan 
        0.391 

Loadings:     ##旋转后的因子载荷矩阵
              Factor1 Factor2               ##公共因子1：就餐环境 ； 公共因子2：红茶
dianmiansheji  0.771         
dianneiqifen   0.889         
nvshengtaidu   0.997         
hongcaiweidao          0.994 
hongcaijiage           0.829 
hongcakougan           0.778 

               Factor1 Factor2
SS loadings      2.384   2.285  ##是公因子fi的方差贡献，即gj^2
Proportion Var   0.397   0.381
Cumulative Var   0.397   0.778  ##分析结果精度

Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 6.38 on 4 degrees of freedom.
The p-value is 0.173 
> fac$scores  ##因子得分
     Factor1    Factor2
A  1.2625054  0.4505873
B  1.3197340 -1.1976950
C  0.3108379  0.4637722
D  0.3175377 -0.3786881
E -0.6048028 -0.4078305            ## 第一公共因子得分最大的A,对本店的就餐环境持有最佳影响
F  1.2837587 -0.3810489
G  1.2616397  0.5258796             ##第二公共因子得分最大的O，对本店的红茶持有最佳印象
H -1.6378828  1.2213928
I -0.6289995 -0.4230391
J -1.5257167 -1.2601339
K -0.5467471 -2.0802990
L  0.2953144  0.4388976
M -0.6579945  0.4834196
N  0.2585119  1.2797300
O -0.7076962  1.2650555

注意：

因子载荷量的统计意义aij ： aij=cov(xi,fj) xi 依赖 fj 的程度
变量共同度的统计意义hi^2 ：hi^2= $\sum$ aij^2 (j=1....m) 是因子载荷矩阵A的第i行元素的平方和，反应的是变量xi对公因子f=(f1,f2,f3,.....fm)T的共同依赖程度。var(xi)=hi^2+ $\psi$ ii
公因子fj方差贡献的统计意义： gj^2= $\sum$ aij^2 (i=1....p) 是因子载荷矩阵A的第j列元素的平方和，是公因子fj对每个变量x1,x2……xp提供方差的总和。gj^2/var(xi) (i=1,2……p)方差贡献率。

补充注意事项：

各公共因子的含义，只能是在做完分析之后，由分析者主观的进行推断
因子载荷量小的变量的处理方法：将这个因变量删除后再进行因子分析；不删除这个因变量，而是将因子载荷量的绝对值为0.5以上逐步下降，直到’任何一个公共因子都不会对某个变量产生太大的影响‘不会发生。通常是0.3到0.5之间的某个

因子载荷量的计算：极大似然法

L = 因变量的个数 + log(x行列式） - x的主对角线上的值的和

使用前提：总体中的数据要服从多变量正态分布
拟合优度检验：ho:公共因子的个数是m ； h1: 公共因子的个数不是m

旋转与varimax法。正交因子模型下： aij=rij

因子载荷量矩阵：公共因子与因变量的因子载荷量

因子结构矩阵：公共因子与因变量的单相关系数

斜交旋转中的promax法

按照varimax法进行旋转
目标因子载荷矩阵
旋转1中的轴，使其靠近2中的目标矩阵
promax法旋转后的因子载荷量矩阵，因子相关矩阵以及因子结构矩阵

因子相关矩阵：公共因子间的单相关系数矩阵

分析结果的精度：排除其他公共因子影响后的贡献；因子结构矩阵的列平方和；相对的
因子得分基于：回归法变量标准化后的数据 × 相关矩阵的逆矩阵 × 因子结构矩阵
能够假定的公共因子个数上限：公共因子个数 <= （ 2*因变量的个数+1-（8×因变量的个数+1）^1/2）/2

主成分分析、因子分析及其有关的数学基础

主成分分析

因子分析

因子载荷量

潜在结构：公共因子

猜你喜欢