二维旋转公式

ros的tf工具包可以很方便的实现任意坐标系之间的坐标转换。但是，如果只是想简单的测试想法，而又不想编写过于庞杂的代码，考虑自己写二维旋转的函数。而与二维旋转问题对偶的另一个问题便是二维坐标系旋转变换。这两个问题的形式基本一样，只是旋转的角度相差一个负号。就是这个容易搞混，所以做个笔记，以备查用。

1. 二维旋转公式（算法）

而（此文只针对二维）旋转则是表示某一坐标点 $(x_1, y_1)$ 某一坐标系下绕原点逆时针（正向）旋转角度 $\theta$ 后得到新的坐标点 $(x_2, y_2)$ 。
在这里插入图片描述

推导：
假定 $v=(x, y)$ , $v'=(x',y')$ ,如上图有 $x=rcos(\phi),y=rsin(\phi),x'=rcos(\phi+\theta),y'=rsin(\phi+\theta)$ (注意，上图有几处错误，坐标轴边上的 $cos/sin(\theta)$ 应改为 $cos/sin(\phi+\theta$ )。展开 $x',y'$ 可得：
$x'=rcos(\phi)cos(\theta)-rsin(\phi)sin(\theta)=xcos(\theta)-ysin(\theta)$
$y'=rsin(\phi)cos(\theta)+rcos(\phi)sin(\theta)=xsin(\theta)+ycos(\theta)$

矩阵形式为: $\left[\begin{matrix}x' \\ y'\end{matrix}\right]=\left[\begin{matrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta)\end{matrix}\right]\left[\begin{matrix}x \\ y\end{matrix}\right]$

则二维旋转矩阵为： $A=\left[\begin{matrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta)\end{matrix}\right] \tag{1}$

void Rotate2(double x1, double y1, double alpha, double& x2, double& y2)
{
	x2 = x1 * cos(alpha) - y1 * sin(alpha);
	y2 = x1 * sin(alpha) + y1 * cos(alpha);
}

2. 二维坐标系旋转变换

假设有一坐标系 $XOY$ ，经过逆时针(正向)旋转角度 $\theta$ 后，得到新的坐标系 $X'O‘Y'$ 。得到原来坐标系中的坐标 $(x,y)$ 在新坐标系下的坐标值被称为坐标系转换。
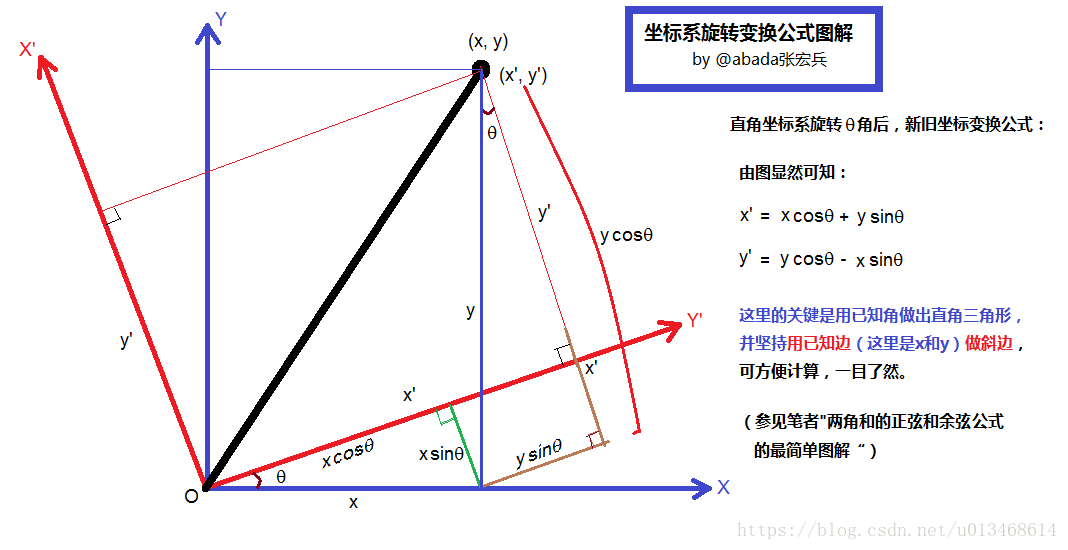
在这里插入图片描述

$x'=xcos(\theta)+ysin(\theta)=xcos(-\theta)-ysin(-\theta)$
$y'=-xsin(\theta)+ycos(\theta)=xsin(-\theta)+ycos(-\theta)$

所以二维坐标旋转变换矩阵为: $B=\left[\begin{matrix} cos(\theta) & sin(\theta) \\ -sin(\theta) & cos(\theta)\end{matrix}\right]=\left[\begin{matrix} cos(-\theta) & -sin(-\theta) \\ sin(-\theta) & cos(-\theta)\end{matrix}\right] \tag{2}$

结论

对比公式（1）与（2），可发现，二维旋转与二维坐标旋转形式一致，只是当旋转都为正向（逆时针）时，角度相差一个负号。也即，在同一坐标轴下将某一点 $(x,y)$ 沿原点正向（逆时针）旋转角度 $\theta$ 后得到的新坐标点 $(x',y')$ ，等价于将点 $(x,y)$ 所在的坐标系 $XOY$ 逆向(顺时针)旋转角度 $\theta$ 后，在新的坐标系 $X'O'Y'$ 下， $(x,y)$ 对应的新坐标点 $(x',y')$ 。拿起纸笔，多摆弄上面两张解释图，就清楚了。