引言

• 并行排序算法可以
  • 以专用并行结构–排序网络
  • 来实现
• $N$输入排序网络
  • 也叫 $N-$sorters，是个有 $N$输入
  • $N$输出的开关电路
  • 对 任意组合 $I=\{i_0,i_1,...,i_{N-1}\}$
  • 输出结果是 $O=\{o_0,o_1,...,o_{N-1}\}$为 $I$的一置换
    • 从小到大哦
  • 排序网络简称排序器
  • 用基本的2-sorters或比较器单元
    • 可构造任意 $N-$sorters
    • 由batcher提出
    • Batcher比较器
• Batcher比较器是个2in2out的比较交换元件
  • 对输入 $A$和 $B$进行比较
  • 大H小L
    

人民研究排序网络基于以下几面

• 构造可完成排序的专门硬件
• 置换网络–N输入置换网络为一个开关电路，它执行 $N\times N$的纵横开关
  • 排序网络本身就实现输入的一置换
• 非适应性排序算法上章已介绍
  • 对很多排序算法
    • 如Shell和快排
    • 基本步骤是俩记录的比较和交换
    • 但比较和交换条件CCI所产生的顺序
      • 部分依赖于记录的初始顺序
      • so shell和快排是适应性算法
  • 也可设计某种排序算法
    • 采用固定的CCI顺序
    • so这算法是非适应性的
    • 用非适应性算法构造排网是研究重点
    • 虽可用适应算法构造排网
      • 但此排网的基本构建不是图3.1中的Batcher比较器
  • 并行排序算法——使用CCI操作的排序算法很适合并行机
    • because只要CCI操作的操作数不同，CCI操作就可同执行

排网性能的俩常参

• 成本和深度
  • 网络所包含比较器数目
  • 从输入到输出的最长路径的比较器数目
    • 也叫延迟级数
• 下图是个4输入排网，3和5
  

成本可考虑的少些，深度更为关注

除了用专用并行结构–排序网络实现排序外

• 还可在通用计算模型下实现并行排序算法
• 并行排序可在共享存储的系统上实现
  • 也可在以互联网络连接起来的
  • 系统上实现
• 互联网络的拓扑结构
  • 决定了处理器间的连接方式
  • 如一维线性阵列
  • mesh结构
  • 树形结构
  • 超立方连接
  • 蝶形连接及洗牌交换网络
  • 互联网络拓扑结构的不同，导致并行算法在其实现上有特殊性

根据并行排序算法的俩实现途径

奇偶归并网络

• Batcher60末提奇偶归并网络
  • 是 两路排序网络的基础
• 设俩代归并的递增序列
  • $<x_1,x_2,...,x_p>$
  • $<y_1,y_2,...,y_q>$
• 一个 $(p,q)$归并器可递归构造如下：
  • 若 $pq=1$，奇偶归并器为图3.1
  • 若 $pq>1$
    • 归并俩奇序 $<x_1,x_3,...,x_{2\lceil p/2\rceil-1}>$
      • 和 $<y_1,y_3,...,y_{2\lceil q/2\rceil-1}>$
      • 得序列 $<v_1,v_2,...,v_{\lceil q/2\rceil+\lceil p/2\rceil}>$
    • 同时归并这俩偶列 $<x_2,x_4,...,x_{2\lfloor p/2\rfloor}>$
      • $<y_2,y_4,...,y_{2\lfloor q/2\rfloor}>$
      • 得到有序序列 $<w_1,w_2,...,w_{\lfloor q/2\rfloor+\lfloor p/2\rfloor}>$
    • 对序列 $<v_1,w_1,v_2,w_2,...,v_{q},w_{q},...v_p>$
      • 进行比较交换操作
        • $w_1:v_2,w_2:v_3,...,w_q:v_{q+1}$
      • 得到最终有序序列

递归构造的奇偶归并网络由三阶段组成

• 一：输出俩有序序列
• 二：两归并网络
• 三：一系列比较单元
• 见图3.3
• 俩归并网络产生俩有序序列V和W哦！
  • 比较器执行比较哦
• 奇偶归并网络深度 $D=1+\lceil log_{2}max(p,q)\rceil$
  • 成本是p和q的复杂函数
  • 但when $p=q=2^t$
    • $C=plog p+1$
    • 可以算一下图3.4深度和成本哦
    • 3和9

举例子1

举例子2

• 怎样把这个技术用到排列数组 $A[]$上呢
• 这意味着我们有办法将 $k-sorters$用到对于 $2组k个数的归并$
• 而且不要额外空间了
  
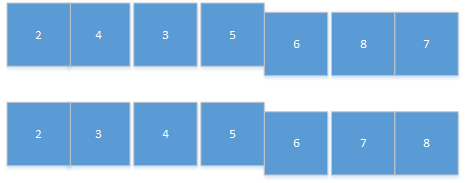
• 下面是对2组4个数的归并
  
• 这样好多了，因为可以对橙色的数字原地排序
  • 蓝色的数据原地排序
  • 变成下面了
  • 然后只需交换就好了
    
    

举例子3

• 已经可以用 $4-sorters$排完8个数了
• 可否用 $4-sorters$排完 $16$个数呢？
  • 当然可以
  • 那么也可以排完任意 $4^k$个数
  • 且这个过程我觉得像堆排序

证明算法正确性

写出算法代码1——感觉一开始写错了

一个细节

• $temp1=(9-6)/2*2+6=8$
• $temp2=2+6+1=9$

• $temp1=2/2*2+6=8$
• $temp2=1/2*2+6+1=7$

odd_even_merge(int A[],int p,int q)
if(p>q) 
{
	int temp1=(q-p)/2*2+p;
	int temp2=(q-p-1)/2*2+p+1;
	odd_even_merge(A[],p,temp1);
	odd_even_merge(A[],p+1,temp2);
}

• 下面就是要把 $A[],p,temp1$
  • 和 $A[],p+1,temp2$
  • 这俩奇偶归并了
  • 感觉上面都写错了哦

写出算法代码2

双调归并网络

• Batcher提奇归网不久
  • 提双归并网
• $x_1,...,x_n$是双调序列
  • 如果
  • (1)存在 $x_k$使得， $x_1\ge...\ge x_k\le...\le x_n$
  • (2)此序列能循环旋转使得(1)满足
• 若输入是双调序列，
  • 则通过双调归并网络
  • 可产生一有序的输出序列
  • 基本原理——Batcher定理

Batcher定理

SS-Mk算法

符号表示

• 有 $k$个有序序列 $k\ge 2$的任意素数
  • 每个序列 $m$个关键字
  • 用 $m \times k$的矩阵 $A$来表示 $k$个带归并的有序序列
  • $0到k-1$， $0到m-1$
  • 列是有序序列哦
    • 且非降
  • 将矩阵 $A$排成行为主的非降有序序列
    • 含意思
    • 每一行非降
    • 且上一行最后一个 $\le$下一行第一个

算法执行

• 多次对 $A$变换
• $A^{t}$
• $A^{0}$表示待变换的矩阵
• 算法每步对 $A$中以一定规律组织起来的元素序列进行排序
  • 但序列元素个数 $\le k$
  • 保证归并过程总可以用k-sorters
• $A(i,j,u,v,c)$
  • 表示 $(a_{i,j},a_{i-u,j+v},...,a_{i-cu,j+cv})$
  • $i,j$起始元素的行列号
  • $u$和 $v$行列跳变值
  • $i-cu\ge 0$
  • $j+cv\le k-1$
• $A^{(t+1)}=SORT(A^{(t)}(i,j,u,v,c))$
  • 啥意思要懂得哦
  • 记得是这个操作是降序啊！！！！！！！！！！
• 算法用到一常数 $r$
  • $r=1+\lceil log(m/k)\rceil$
• for i in [X,Y] do
  • 啥意思
  • 并行的意思
• for i=A to Y do
  • 串行

Sloping-and-Shanking Multiway Merging的描述

• $for \quad i \quad in [0,m-1] do$
  • $A^{(1)}(i,k-1,0,-1,k-1)=$
  • $SORT(A^{(0)}(i,k-1,0,-1,k-1));$
  • 越加-1越小，左边的就小哦
  • 并行对每行进行排序

• for t=1 to r do{ $r=1+\lceil log(m/k)\rceil 例子等于3$}
  • for i in [0,m-1] do
    • $c=min([i*2^{r-t}],k-1)$
    • $A^{t+1}(i,0,2^{r-t},1,c)=SORT(A^{t}(i,0,2^{r-t},1,c))$
    • 每行第一个元素开始 $2^{r-t}$是向上（越小啊）
    • 1表示向右（越小）
    • 进行排序
  • $for \quad i \quad in [m-2^{r-t},m-1]\land( j \quad in\quad[1,k-2] )$
    • $c=min(k-1-j,\lfloor i/2^{r-t}\rfloor)$
    • $A^{t+1}(i,j,2^{r-t},1,c)=SORT(A^{t}(i,j,2^{r-t},1,c))$
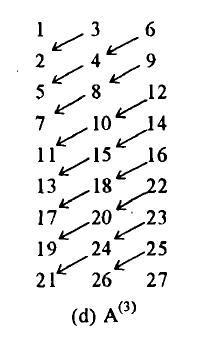
    • 作用你知道哦
  • 斜率是 $2^{3-1}$。。。 $2^{0}$
    
    
• for v=2 to k-1 do
  • for

Algorithm SS-Mk
	Input:k个非降，用A[0:m-1,0:k-1]
	Output:不说了
	for i in [0,m-1] do
		A^(1)(i,k-1,0,-1,k-1)=SORT(A^(0)(i,k-1,0,-1,k-1));

算法时复度

• k-sorters时间 $t_k$
• 算法时间复杂度
  • $(1+r+k-2)t_k=(k+\lceil log(m/k)\rceil)t_k$
  • $=(k+\lceil log(N/k^2)\rceil)t_k$

重大意义

• 那么如果我有好多数据
• 比如

$SS-M_k$正确性

• $X=(X_1,...,X_m)$
  • $Y=(Y_1,...,Y_n)$为两非降(升)序列
• $X'=(X'_1,...,X_m')$
  • $Y'=(Y'_1,...,Y_n')$为X和Y的任意排列
  • 对这俩组数，证明关系稳定性定理定理12和推理12
  • $\theta$表 $\le$或 $\ge$

定理1

• $m=n$时，如 $x_p'\theta y_p'$（应该是对任意p都成立的）
  • 则 $x_p\theta y_p$（ $1\le p\le n$）
  • 很好理解啊，
  • 假设 $\theta$是 $\le$
  • 如果前者成立，那么对于 $x_p$来说， $X$里面最多p-1个人小于我
  • 所以 $X'$里面最多p-1个人小于我
    • 是 $x_1...x_{p-1}$
    • 这导致
    • $Y'$里面最多也就是p-1个人小于我
  • 而 $y_p$排行老p
  • 所以好啦！
  • 假设 $\theta$是 $\ge$
  • 对称的哦

推论1

• $m=n$，如果 $(x_p'\theta y_p')$ $(1\le p\le n)$
  • 及 $(x_p'\theta y_{p-1}')$ $(2\le p\le n)$
• 则 $(x_p\theta y_p)$ $(1\le p\le n)$
  • $(x_p\theta y_{p-1})$ $(2\le p\le n)$
• 对于 $(2\le p\le n)$的 $x_p$，假设 $\theta$= $\le$
  • 那么 $X'$里面至少有n-p个人大于等于它
  • 根据下图可知 $Y'$至少有n-p+1个人 $\ge$它
  • 所以 $x_p\le y_{p-1}$