Description

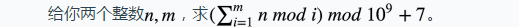
Input

Output

Solution

整除分块：https://blog.csdn.net/gdhy9064/article/details/90112836

通过整除分块，我们可以得到对于每个x $\left\lfloor\frac{n}{x}\right\rfloor$的值，那么可以转化原式：

$\sum_{i=1}^nn \mod i=\sum_{i=1}^ni*n-\left\lfloor\frac{n}{x}\right\rfloor*x$。

利用等差数列公式，可以在 $O(\sqrt{n})$的时间复杂度内计算 $\sum_{i=1}^{\min(n,m)}$的值。
若m>n，那么加上 $(m-n)*n$就好了。

Code

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
long long n,m,ans,l=1,r;
int main(){
	scanf("%lld%lld",&n,&m);
	while(l<=n&&l<=m){
		r=min(n/(n/l),m);
		long long sum1,sum2;
		sum1=(r-l+1)%mod*(n%mod)%mod;
		if((r-l)%2==1) sum2=((r-l+1)/2%mod*((l+r)%mod)%mod*((n/l)%mod)%mod)%mod;
		else sum2=(((l+r)/2%mod)*((r-l+1)%mod)%mod*((n/l)%mod)%mod)%mod;
		ans=(ans+(sum1-sum2+mod)%mod)%mod;
		l=r+1;
	}
	if(n<m) ans=(ans+(m-n)%mod*(n%mod)%mod)%mod;
	printf("%lld",ans);
}