【学习笔记】线段树详解（全）

和三个同学一起搞了接近两个月的线段树，头都要炸了T_T，趁心态尚未凉之前赶快把东西记下来。。。

【目录】

• 【基础】作者：(Silent(Silent_EAG)EAG)
• 【懒标记】作者：(Silent(Silent_EAG)EAG)
• 【扫描线】作者：(IC(IC_QQQ)QQQ)
• 【权值线段树】作者：(Xing(Xing_Ling)Ling)
• 【动态开点】作者：(Xing(Xing_Ling)Ling)
• 【线段树合并】作者：(Xing(Xing_Ling)Ling)
• 【可持续化线段树—静态主席树】作者：(Xing(Xing_Ling)Ling)
• 【可持续化线段树—动态主席树(岂可修)】作者：(Xing(Xing_Ling)Ling)

一：【基础姿势】

piaopiao 一下隔壁大佬的文章QAQ: SilentSilent_EAGEAG

基础题走起：

• 【模板】线段树 11 [P3372][P3372] 【标签】线段树/树状数组 【题解】SilentSilent_EAGEAG

• CanCan youyou answeranswer thesethese queriesqueries II [SP1043][SP1043] 【标签】线段树

• IntervalInterval GCDGCD [CH4302][CH4302] 【标签】线段树/树状数组/GCDGCD 【题解】SilentSilent_EAGEAG

高档题走起：

• CanCan youyou answeranswer thesethese queriesqueries IIIIII [SP1716][SP1716] 【标签】线段树/懒标记 【题解】SilentSilent_EAGEAG

• 炸勃龙 II [P4118][P4118] [BZOJ5394][BZOJ5394] // 奈芙莲·卢可·印萨尼亚 NephrenNephren RuqRuq InsaniaInsania [P3934][P3934] 【标签】线段树/树状数组/暴力枚举/数论/欧拉定理 （YNOI2016YNOI2016 毒瘤数论）

二：【懒标记】

见隔壁：SilentSilent_EAGEAG

基础题走起：

• 【模板】线段树 22 [P3373][P3373] // 维护序列 [P2023][P2023] [BZOJ1798][BZOJ1798] 【标签】线段树/懒标记 【题解】SilentSilent_EAGEAG

高档题走起：

• CanCan youyou answeranswer thesethese queriesqueries IIIIIIII [SP2713][SP2713] 【标签】线段树/懒标记 【题解】SilentSilent_EAGEAG

• 市场 [LOJ6029][LOJ6029] 【标签】线段树/懒标记 【题解】SilentSilent_EAGEAG

• 酒店 HotelHotel [P2894][P2894] [BZOJ1593][BZOJ1593] 【标签】线段树/懒标记

• 序列操作 [P2572][P2572] [BZOJ1858][BZOJ1858] 【标签】线段树/懒标记/珂朵莉树 （如果尝试用线段树做的话，懒标记的运用达到了毁天灭地的地步。而珂学就爽了，那么它就是道大水题）

三：【扫描线~】

见隔壁：ICIC_QQQQQQ

四：【权值线段树】

 QAQ:以前似乎在某个地方看到过一个叫做做权值树状数组的东西唉QWQ
  DL:其实他们都是一样的思想，只是不同的实现方式而已
 
 QAQ:可是XX在写过无数区间作业的题后，发现无论是哪一类，树状数组都比线段树快不止三倍唉QWQ
  DL:*****

权值线段树是什么？

权值线段树，顾名思义是一颗线段树。 但它和普通线段树略有不同： 普通线段树维护的是一段区间的数值的总和或最大值等等...... 而权值线段树维护的是一定范围内某个数值出现的次数。实际上它和之前的权值树状数组是一样的原理。（求逆序对也可用权值线段树实现 ）

它有什么用？

按照定义，我们可以用它对于权值进行计数，感觉有点像数位dpdp吧，求一定范围内符合要求的数的个数。权值线段树的$“范围范围”是不定的，而是不定的，而“要求要求”$一般是：在给定的数值范围内。

举个栗子： 有一个数列： a(1,1,2,3,3,4,4,4,4,5)a(1,1,2,3,3,4,4,4,4,5) 对其维护一个计数的权值线段树，树的大小就是数列的值域 [mins～maxs][mins～maxs]，即 [1～5][1～5]。

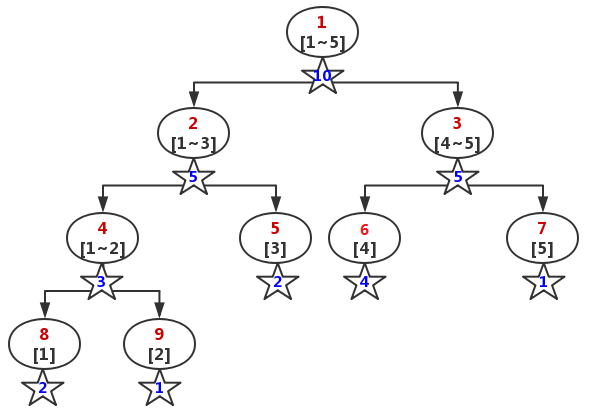
如图，在数列中： 数值 11 出现了 22 次 数值 22 出现了 11 次 数值 33 出现了 22 次 数值 44 出现了 44 次 数值 55 出现了 11 次

重要应用：

在此基础上，它还有一个很重要的作用 ： 查询某区间内第 kk 小或第 kk 大的值。

引理：

如果在值域范围内 (( 即 [mins～maxs][mins～maxs] ))中发现有某个位置 xx，数列中存在这个数 xx，且使得数值范围在区间 [mins～x][mins～x] 内的数一共有 kk 个，那么 xx 就是第 kk 小的数。 反之亦然： 如果在值域范围内 (( 即 [mins～maxs][mins～maxs] ))中发现有某个位置 xx，数列中存在这个数 xx，且使得数值范围在区间 [x～maxs][x～maxs] 内的数一共有 kk 个，那么 xx 就是第 kk 大的数。

【分析】

以查询第 kk 小为例

我们可以用一种二分的思想，当需要在某个值域范围 [l～r][l～r] 内查找第 kk 小时，先计算出数值在 [l～mid][l～mid] 以内的数的个数 tmptmp，再将其与 kk 进行比较：

• 如果 tmp⩾ktmp⩾k，则说明第 kk 小的数应存在于 [l～mid][l～mid] 这个范围。
• 如果 tmp⩽ktmp⩽k，则说明第 kk 小的数应存在于 [mid+1～r][mid+1～r] 这个范围，而实际上就等价于在 [mid+1～r][mid+1～r] 中找到第 k−tmpk−tmp 小的数。

【Code】

#define Re register int
#define pl tree[p].PL
#define pr tree[p].PR inline int ask(Re p,Re L,Re R,Re k){//查询第k小 if(L==R)return L;//边界叶节点 Re tmp=tree[pl].g;//计算左子树(数值范围在L~mid的数)共有多少个数字 if(tmp>=k)return ask(pl,L,mid,k); //左子树已经超过k个，说明第k小在左子树里面 else return ask(pr,mid+1,R,k-tmp); //左子树不足k个数字，应该在右子树中找到第(k-tmp)小 } 

五：【动态开点】

什么是动态开点？

动态开点用法较固定，目的也很明确：节省空间。 它的实质其实就是在空间不够的情况下，把不需要的节点变成虚点。

有什么用？

求解逆序对时可以用权值树状数组，那么如果尝试用权值线段树做的话会出现什么后果呢？

肯定是可解的。但是，由于值域大多都是 infinf 级别的数字，况且某些比较毒瘤的在线操作还没法离散化，于是在使用权值线段树时，一般都会伴随着动态开点的使用。

如何使用？

这里引用一下一位大佬的比喻： 开局一个根，枝叶全靠给。

当要用到(一般只有修改)某个节点的信息时，就手动开一个新的节点，给它一个点的空间包括各种节点信息。而在查询中如果发现进入的节点不存在(还没开发过)，那么直接返回，不需要在查询时新建节点。

【空间复杂度】

Q∗log(inf)Q∗log(inf)。其中 QQ 为修改次数。

【Code】

（基本框架）

int cnt;
inline void sakura(Re &p,Re L,Re R,Re ???){//【???修改】 if(!p)p=++cnt,tree[p].?=???; //发现进入了一个空节点,新建一个节点，赋予它编号,记录基本信息 if(L==R){tree[p].?=???;return;} //达到叶子节点，记录一些特殊的信息，并返回 Re tmp=???;//可能会在在递归之前进行一些计算来方便判断 if(???)sakura(pl,L,mid,???);//递归进入左子树 if(???)sakura(pr,mid+1,R,???);//递归进入右子树 tree[p].?=???;//回溯后更新信息 } 

六：【线段树合并】

什么是线段树合并？

简单来说就是将两棵线段树合并起来，并累加它们的信息。

有什么用？

线段树合并一般用于对树上信息的统计，例如：对一棵树的所有叶子节点都开一个线段树，统计信息时，将所有的儿子节点的线段树合并起来，得到父亲节点的线段树，再用其去合并统计祖先的信息。

【时间复杂度】

如果一棵线段树的所有节点都不为空（动态开点会使得虚点的存在），离散化后值域为 nn，递归一棵线段树树的时间复杂度达到最大： O(logn)O(logn)。如果总共 nn 棵树的所有节点都不为空，那么需要合并 n−1n−1 次， 总时间复杂度达到最大： O(n∗logn)O(n∗logn)。

七：【可持续化线段树—静态主席树】

来看一道经典的例题 【模板】可持久化线段树 11 (主席树) [3834][3834] // KK-thth NumberNumber [P3834][P3834] [POJ2104][POJ2104] [SP3946][SP3946]

【题目大意】

给定一个长为 nn 的数列以及 QQ 个查询，每次查询输入两个整数 ll,rr，输出数列中 ll ~ rr 第 KK 小的数。

【 分析】

此题有三个关键点：

1. 求一棵数列中的第 KK 大或第 KK 小的数。 解决方案：权值线段树

2. 如果仅仅是这样，则非常好办，给出的询问是一段区间。一段长为 nn 的数列中共有 n(n−1)/2n(n−1)/2 个不同的区间，如果给每个区间都开一个权值线段树，后果是：TLETLE ++ MLEMLE ++ 初始化建树无从入手。解决方案：前缀和 （对于原数列的每个位置都建立一个权值线段树，p[i]p[i] 表示第 ii 个位置上的树的根节点编号，用 tree[pt[i]]tree[pt[i]] 表示从第 11 个到第 ii 个数这个区间中共 ii 个数所维护成的一棵权值线段树。message[pt[i]]=∑ij=1message[pt[j]]message[pt[i]]=∑j=1imessage[pt[j]]）

3. 可内存还是远远不够，即使是使用了【动态开点】 ++ 离散化，值域由 infinf 降为 NN，每一棵权值线段树的节点数降为 N∗2N∗2，节点，但一共有 NN 棵树，N∗N∗2N∗N∗2 动辄就是几十万兆内存。（做一个简单的计算： $200000200000243/1024/1024 \thickapprox 305175.78125 Mb$） 解决方案：可持续化由于第 ii 棵树 tree[pt[i]]tree[pt[i]] 与第 i−1i−1 棵树 tree[pt[i−1]]tree[pt[i−1]] 只有 lognlogn 个节点不一样，于是只需要对第 i−1i−1 棵树进行一次单点修改将 a[i]a[i] 加入，就变成了第 ii 棵树。因此我们可以由已经建好第 i−1i−1 棵树迅速建立起第 ii 棵树，这也就是主席树思想的精髓所在。 说具体点，就是让第 ii 棵树与第 i−1i−1 棵树公用一些节点（因为在这些没有发生改变的部分，它们的信息是完全相同的），在递归过程建树中，如果发现要进行【单点修改】操作的是左子树，那就让新树的右子树编号指向旧树的右子树编号（即 tree[pt[i]].pr=tree[pt[i−1]].prtree[pt[i]].pr=tree[pt[i−1]].pr ）然后递归进入左子树的建立，反之亦然。 但第 11 棵树需要由第 00 棵树变化而来，当有特殊需要时，要提起把第 00 棵树建立完整，而道题不需要，因为第 00 棵树本来就为空，所以不用管。

【时间复杂度】

每次建树的过程都接近于【单点修改】， 为 O(logn)O(logn) ,所以初始化建树的过程为 O(nlogn)O(nlogn) 。

单次询问采用权值线段树中的【查询第 kk 小】，为 O(logn)O(logn)。

总共 QQ 次询问，为 O(Qlogn)O(Qlogn) 。

总时间复杂度： O((n+Q)logn)O((n+Q)logn)

【空间复杂度】

如果要建立完整的第 00 棵树，会占用 n∗2n∗2 个节点，每棵新树的建立都要新建 lognlogn 个节点，一共有 nlognnlogn。

总空间复杂度：(logn+2)∗n