欧几里得算法

int gcd(int a,int b)
{
     if(b==0)
     {
         return a;
     }
    return gcd(b,a%b);
}

拓展欧几里得算法

最主要的核心就是 x=y y=x-a/b*y

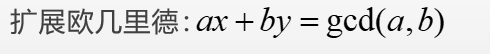
int ex_gcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {           
        x=1;
        y=0;
        return a;
    }
    int g=exgcd(b, a%b, x, y);
    int temp=y;
    x=temp;
    y=x-(a/b)*y;        
    return r;
}

但此时得到 下，y是一组特解

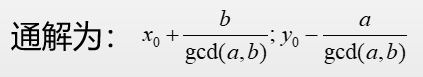
并且，此时得到的x特解不一定是最小非负整数解
最小
非负整数解 ：x=（x% (b/gcd(a,b) +(b/gcd(a,b) )% (b/gcd(a,b);

拓展

最小非负整数解同上面的求法一样

解同余式

解的个数
通解为 x=x+m/g*k
虽然对于方程 ax+my=c 来说，k可以取任意整数，但是对于同余式来说解在模m的意义下是相同的，所以只需要找出那些在模m下意义不同的解 因此只需要考虑可分别取 0 1 2 3…gcd(a,m)-1;

逆元

对于 （b/a)%m 的求解 .
有时，在b是特别的大，在求b的过程中需要对b取模，但是除法是不可以对b直接取模的，因此，就需要找a的逆元把除法转换为乘法

逆元 x: ax==1(modm)

成立的条件

1. a|b b能够整除a
2. gcd(a,m)=1

int inverse(int a,int m)
{
	int x,int y;
	int g=ex_gcd(a,m,x,y);
	return (x%m+m)^m;	
}