研究论文《Joint Scheduling and Deep Learning-Based Beamforming for FD-MIMO Systems Over Correlated Rician Fading》

摘要: 本文研究了在相关瑞利衰落信道下的全维多输入多输出系统的下行传输问题。通过在基站获取的统计信道状态信息，每个用户的波束形成向量通过解耦彼此分离直至达到平均信噪比下界的最大值，推导出了最优波束形成矢量，该矢量涉及两个方向的视距分量和相关矩阵。为了减少获得每个用户波束向量的时间使用深度学习算法。基于所提出的波束形成方法，对每个用户的遍历率进行分析，并给出简单的封闭近似，对评价系统性能和用户调度有很大的帮助。此外提出两种最不相似和最小干扰信号因子的用户调度算法，与基于和速率的贪心调度算法相比，大大降低了算法复杂度。

系统模型

本文中，我们考虑的是单个的FD-MIMO下行传输系统，系统中有 $L$个单天线用户终端。基站采用 $M \times N$型的均匀平面天线阵（UDP），每一行和每一列中相邻的两个天线单元之间的距离为载波 $\lambda$的一半，基站最多可以为 $U_t$个用户服务。则用户u处接收到的信号可以表示为：
$y_{u}=\sqrt{p_{u} \mathbf{h}_{u}^{T}} \mathbf{w}_{u} x_{u}+\sum_{i=1, i \neq u}^{U_{t}} \sqrt{p_{i} \mathbf{h}_{u}^{T}} \mathbf{w}_{i} x_{i}+n_{u}$
其中， $\mathbf{h}_{u} \in \mathbb{C}^{M N \times 1}$表示基站中的信道向量， $\mathbf{w}_{i} \in \mathbb{C}^{M N \times 1}$表示用户i的标准波束形成矢量， $x_i$表示用户i满足 $\mathrm{E}\left\{\left|x_{i}\right|^{2}\right\}=1$的数据符号， $n_{u} \sim C N\left(0, \sigma_{u}^{2}\right)$是复高斯白噪声， $p_i$是在总功率限制 $\sum_{i=1}^{U_{t}} p_{i} \leq P_{t}$下为用户i传输功率.

本文中研究相对一般的信道模型，即相关衰落信道模型。基站中用户间的信道矢量 $\mathbf{h}_{u}$可表示为 $\mathbf{h}_{u}=\sqrt{\frac{K_{u}}{K_{u}+1}} \overline{\mathbf{h}}_{u}+\sqrt{\frac{1}{K_{u}+1}} \tilde{\mathbf{h}}_{u}$其中 $\overline{\mathbf{h}}_{u} \in \mathbb{C}^{M N \times 1}$表示视距分量， $\tilde{\mathbf{h}}_{u} \in \mathbb{C}^{M N \times 1}$表示瑞利分布的非视距分量， $K_{u}$表示LOS和非LOS信道功率的比率。在给定的UPA中，确定部分 $\overline{\mathbf{h}}_{u}$可表示为： $\overline{\mathbf{h}}_{u}=\mathbf{a}_{H, u}\left(\theta_{u}, \varphi_{u}\right) \otimes \mathbf{a}_{V, u}\left(\theta_{u}\right)$
with
$\begin{aligned} \mathbf{a}_{H, u}\left(\theta_{u}, \varphi_{u}\right) &=\left[1, e^{-j \pi \phi_{u}}, \cdots, e^{-j \pi(N-1) \phi_{u}}\right]^{T} \\ \mathbf{a}_{V, u}\left(\theta_{u}\right) &=\left[1, e^{-j \pi \sin \theta_{u}}, \cdots, e^{-j \pi(M-1) \sin \theta_{u}}\right]^{T} \end{aligned}$
其中 $\phi_{u}=\cos \theta_{u} \sin \varphi_{u}, \theta_{u}$ 和 $\varphi_{u}$ 分别是用户 $u$ 在竖直以及水平方向的倾斜角 (AoD)。通过引用资料可得，非LOS分量可表示为：
$\tilde{\mathbf{h}}_{u}=\left(\mathbf{R}_{H, u}^{1 / 2} \otimes \mathbf{R}_{V, u}^{1 / 2}\right) \mathbf{h}_{w, u}$
其中 $\mathbf{h}_{w, u} \in \mathbb{C}^{M N \times 1}$的项是独立同分布的具有零均值和单位方差的复高斯随机变量(RVs)， $\mathbf{R}_{H, u} \in \mathbb{C}^{N \times N}$和 $\mathbf{R}_{V, u} \in \mathbb{C}^{M \times M}$分别是水平和竖直信道的相关矩阵。此外，我们假设每个单用户都拥有各自的有效CSI，而基站有所有用户的统计CSI，即 $K_{u}, \sigma_{u}^{2}, \overline{\mathbf{h}}_{u}, \mathbf{R}_{H, u}, \mathbf{R}_{V, u}$,这些都可以通过基站对FDD系统的长期反馈来获得。

下行波束形成传输

在我们所研究的下行传输系统中，遍历和率可表示为： $R_{\mathrm{sum}}=\sum_{u=1}^{U_{t}} R_{u}$
$R_u$是用户u的遍历和率，可表示为：
$R_{u}=E\left\{\log _{2}\left(1+\frac{\frac{P_{t}}{U_{t}}\left|\mathbf{h}_{u}^{T} \mathbf{w}_{u}\right|^{2}}{\sigma_{u}^{2}+\frac{P_{t}}{U_{t}} \sum_{i=1, i \neq u}^{U_{t}}\left|\mathbf{h}_{u}^{T} \mathbf{w}_{i}\right|^{2}}\right)\right\}$但是公式中的元素在相关衰落信道下很难获取。


受深度学习技术在无线通信中的新兴应用启发，我们计划通过深度神经网络来解决波束形成问题。当天线和用户数量增加时，传统的数据驱动DL方法会导致神经网络变得非常庞大和复杂，这需要大量的训练时间和庞大的训练数据集。为了减少网络的复杂性和训练数据的获取,以及大量的训练数据,我们分离计算并推导出结构每个用户的波束成形向量通过最优度量，即最大化信漏噪比(SLNR)。在此基础上，提出了基于模型驱动的深度学习波束形成算法和解析波束形成算法。

A. 波束成形架构

用户u 的SLNR可表示为:
$\operatorname{SLNR}_{u}=\frac{\frac{P_{t}}{U_{t}}\left|\mathbf{h}_{u}^{T} \mathbf{w}_{u}\right|^{2}}{\sigma_{u}^{2}+\frac{P_{t}}{U_{t}} \sum_{i=1, i \neq u}^{U_{t}}\left|\mathbf{h}_{i}^{T} \mathbf{w}_{u}\right|^{2}}$最后可推导为 $\mathrm{SLNR}_{u}^{L}=\frac{\frac{P_{t}}{U_{t}} \mathbf{w}_{u}^{H} \Delta_{u} \mathbf{w}_{u}}{\sigma_{u}^{2}+\frac{P_{t}}{U_{t}} \sum_{i=1, i \neq u}^{U_{t}} \mathbf{w}_{u}^{H} \Delta_{i} \mathbf{w}_{u}}$
其中
$\begin{aligned} \Delta_{i}=& \frac{1}{K_{i}+1} \mathbf{R}_{H, i}^{T} \otimes \mathbf{R}_{V, i}^{T}+\frac{K_{i}}{K_{i}+1} \overline{\mathbf{A}}_{H, i} \otimes \overline{\mathbf{A}}_{V, i} \\ & i=1, \cdots, U_{t} \\ \overline{\mathbf{A}}_{H, i}=& \mathbf{a}_{H, i}^{*}\left(\theta_{i}, \varphi_{i}\right) \mathbf{a}_{H, i}^{T}\left(\theta_{i}, \varphi_{i}\right) \end{aligned}$
并且
$\overline{\mathbf{A}}_{V, i}=\mathbf{a}_{V, i}^{*}\left(\theta_{i}\right) \mathbf{a}_{V, i}^{T}\left(\theta_{i}\right)$
定义
$\begin{array}{l} {\Lambda_{H, u}=\mathbf{F}_{N}^{H} \mathbf{R}_{H, u}^{T} \mathbf{F}_{N}} \\ {\Lambda_{V, u}=\mathbf{F}_{M}^{H} \mathbf{R}_{V, u}^{T} \mathbf{F}_{M}} \\ {\mathbf{A}_{H, u}=\mathbf{F}_{N}^{H} \overline{\mathbf{A}}_{H, u} \mathbf{F}_{N}} \end{array}$
且
$\mathbf{A}_{V, u}=\mathbf{F}_{M}^{H} \overline{\mathbf{A}}_{V, u} \mathbf{F}_{M}$
其中 $\mathbf{F}_{N} \in \mathbb{C}^{N \times N}$和 $\mathbf{F}_{M} \in \mathbb{C}^{M \times M}$都是统一DFT矩阵.对于大型均匀直线天线阵,其相关矩阵的特征向量可以用DFT矩阵近似，只有少数相邻的特征值非零。最后我们可以得到SLNR下界的表达式为
$\mathrm{SLNR}_{u}^{L} \leq \frac{\rho_{u}}{U_{t}}\left(\frac{\lambda_{H, u}^{\left(\bar{n}_{u}\right)} \lambda_{V, u}^{\left(\bar{m}_{u}\right)}}{K_{u}+1}+\frac{K_{u} a_{H, u}^{\left(\bar{m}_{u}\right)} a_{V, u}^{\left(\bar{m}_{u}\right)}}{K_{u}+1}\right)$
其中 $\rho_{u}=P_{t} / \sigma_{u}^{2}, \lambda_{H, u}^{(i)}$ 和 $\lambda_{V, u}^{(i)}$ 是 $\Lambda_{H, u}$ and $\Lambda_{V, u}第$i $个对角元素, a_{H, u}^{(i)}$和 $a_{V, u}^{(i)}$ 是 $\mathbf{A}_{H, u}$ and $\mathbf{A}_{V, u}第$i $个对角元素$, $\bar{m}_{u}$和 $\bar{n}_{u}$是矩阵 $\Omega_{u}$最大元素的索引值 $(i, j)$ - $\omega_{u}^{(i, j)}$ :
$\omega_{u}^{(i, j)}=\frac{1}{K_{u}+1} \lambda_{V, u}^{(i)} \lambda_{H, u}^{(j)}+\frac{K_{u}}{K_{u}+1} a_{V, u}^{(i)} a_{H, u}^{(j)}$
$\omega_{u}^{\left(\bar{m}_{u}, \bar{n}_{u}\right)}=\max _{1 \leq i \leq M, 1 \leq j \leq N} \omega_{u}^{(i, j)}$
SLNR表达式只在且仅当基站用波束形成向量传输给用户u时实现
$\mathbf{w}_{u}=\left(\mathbf{F}_{N}\right)_{\bar{n}_{u}} \otimes\left(\mathbf{F}_{M}\right)_{\bar{m}_{u}}$
用户i(i≠u)应该满足 $\displaystyle \omega_{i}^{(\mathrm{m}_{u},\mathrm{n}_{u})}=\min_{1\leq m\leq M,1\leq n\leq N}\omega_{i}^{(m,n)}=0.$的条件.

基于以上分析后,将 $\mathbf{w}_{u}$作为我们想要得到的波束赋形向量.

B. 基于深度学习的波束成形算法

由此我们可以得出求波束赋形向量 $\mathbf{w}_{u}$的关键是求出 $\mathrm{m}_{\mathrm{u}}$和 $\mathrm{n}_{\mathrm{u}}$.为了降低计算复杂度和时间,我们采用深度学习算法.

1. 深度学习神经网络架构
   $\mathbf{w}_{u}$可分为竖直和水平两个方向分别进行计算,由之前推导可知, $\overline{n}_{\mathrm{u}}$和 $\overline{m}_{\mathrm{u}}$只有关于 $\lambda_{H,\mathrm{u}}^{(i)}, a_{H,\mathrm{u}}^{(i)}, i= 1$. . . , N, $N, \lambda_{V,\mathrm{u}}^{(j)}, a_{V,\mathrm{u}}^{(j)},j=1, \cdots$ , $M$ 和 $K_{\mathrm{u}}$.

我们构建前向传播深度神经网络(BFDNN)来对这两个未知量进行计算.

输入值为 $\mathrm{x}_{\mathrm{u}}= \{K_{\mathrm{u}},\ \lambda_{H,\mathrm{u}}^{(i)},\ a_{H,\mathrm{u}}^{(i)},\ \lambda_{V,\mathrm{u}}^{(j)},\ a_{V,\mathrm{u}}^{(j)}|i=1,\ \cdots,\ N,j=1,\ \cdots,\ M\}$,这些都可以在基站中获取到.

网络输出值为 $\mathrm{p}_{\mathrm{u}} \in \mathbb{R}^{(N+M)\times 1}$,取值为0或1
直接上图:




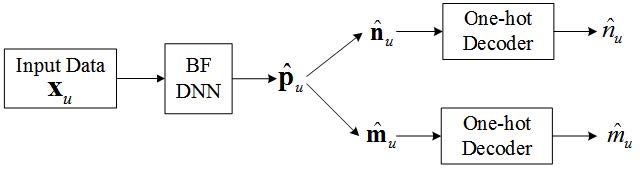
最后的输出值可表示为 $\mathrm{P}_{\mathrm{u}}=f(\mathrm{x}_{\mathrm{u}},\ \theta)=f^{(3)}(f^{(2)}(f^{(1)}(\mathrm{x}_{\mathrm{u}})))$
网络一共分为四层,即输入层,隐含层,dropout层和输出层.
- 输入层: 即输入之前在基站中获取的必要数据集;
- 隐含层: 使用Relu非线性激活函数, $f_{R}(x)=\displaystyle \max(0,\ x)$. 第i个神经元输出为 $z_{i}^{(1)}=f_{R}(\displaystyle \sum_{j}w_{i,j}^{(1)}x_{\mathrm{u}\iota}^{(j)}+b_{i}^{(1)}), i=1, \cdots, N_{1}$
- dropout层: 防止在训练过程中数据过拟合.依旧使用Relu非线性激活函数. 第i个神经元输出为 $z_{i}^{(2)}=f_{R}[r_{i}(\displaystyle \sum_{j}w_{i,j}^{(2)}z_{j}^{(1)}+b_{i}^{(2)})], i=1, \cdots, N_{2}$
$r_{i}\sim Bernoulli(P)$是指 $r_i$有P的概率为0.
- 输出层: 分别包含水平概率向量所有可能的水平索引值和垂直概率向量所有可能的垂直索引值. 激活函数是S型函数,即 $f_{\mathrm{S}}(\mathrm{x})_{i}= 1/(1+e^{-x_{i}})$, $\mathrm{x}=[x,\ x,\ \cdots\ ,\ x_{N+M}]^{T}$.第i个输出可表示为 $p_{\mathrm{u},i}=f_{\mathrm{S}}(\mathrm{g})_{i},\ i=1,\ \cdots\ ,\ N+M$
$g_{i}= \displaystyle \sum_{j}w_{i,j}^{(3)}z_{j}^{(2)}+b_{i}^{(3)}, w_{i,j}^{(3)}$是连接前层第i个神经元的第j个输出的权重.

2. 训练过程
BFDNN(波束赋形深度神经网络)是监督学习使用前向传播算法去寻找适当的参数集的神经网络.

从DNN按不同层的位置划分，DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层，如下图示例，一般来说第一层是输入层，最后一层是输出层，而中间的层数都是隐藏层。

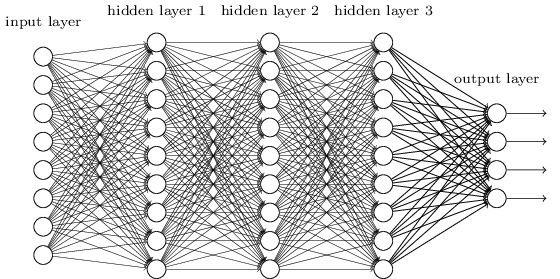
层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。

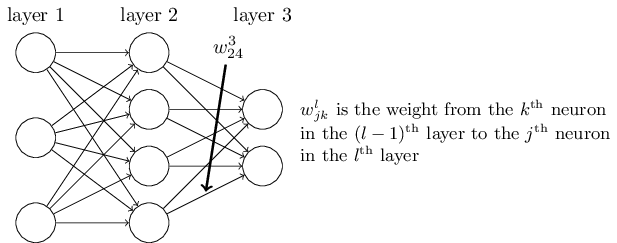
我们可以利用上一层的输出计算下一层的输出,也就是所谓的DNN前向传播算法.DNN的前向传播算法也就是利用我们的若干个权重系数矩阵WW和偏倚向量bb来和输入值向量xx进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为止 。

• 首先我们随机生成一组输输入参数集 $\mathrm{x}_{\mathrm{u}}= \{K_{\mathrm{u}},\ \lambda_{H,\mathrm{u}}^{(i)},\ a_{H,\mathrm{u}}^{(i)},\ \lambda_{V,\mathrm{u}}^{(j)},\ a_{V,\mathrm{u}}^{(j)}|i=1,\ \cdots,\ N,j=1,\ \cdots,\ M\}$
• 接下来我们得到了对应的水平索引和数值索引
• 最后我们通过one-hot编码法对 $\overline{n}_{\mathrm{u}}$和 $\overline{m}_{\mathrm{u}}$进行编码得到训练标签 $\overline{p}_{\mathrm{u}}$

通过采用监督学习的方法，该网络经过训练，使分类交叉熵(CE)损失函数最小化。分类交叉熵一般使用损失函数去测量目标和输出预测值的差距,被定义为:
$L(\displaystyle \theta)=\frac{-1}{U}\sum_{i=1}^{U}\sum_{k=1}^{N+M}[\overline{p}_{i,k}\ln(\hat{p_{i,k}})+(1-\overline{p}_{i,k})\ln(1-\hat{p}_{i,k})]$
U是训练样本数, $\overline{p}_{i,k}$是 $\overline\bold{p}_{i}$的第k个元素.

BFDNN由于不同用户的波束形成向量是解耦的，与调度结果无关,所以对所有用户可以通过单个线下训练实现.计算由线上转为了线下,所以大大减小了计算复杂度.它还可以在不需要重复训练的情况下处理各种各样的环境，因为它同时考虑了LOS和相关性的影响。

以上内容为论文中关于数据驱动算法求解波束成形问题的讲解,下面的内容是关于模型驱动求解以及解决用户调度的问题,我会在接下来的文章中继续进行分析.

对于本文的数据驱动算法求解波束赋形向量中,使用BFDNN对非线性模型进行预测,运用了DNN前向传播算法.

所谓的DNN前向传播算法就是利用若干个权重系数矩阵W,偏倚向量b来和输入值向量x进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为值。

输入: 总层数L，所有隐藏层和输出层对应的矩阵W,偏倚向量b，输入值向量x
输出：输出层的输出。

因为本论文中研究的模型较为简单,数据集较易获取,输出值只为0或1,所以就直接采用较为简单的前向传播算法进行训练.

同时我们要注意几个非线性回归的基本要素:

• 模型: 这里我们使用的BFDNN模型
• 数据集: 这里我们的输入数据集就是我们在基站中所采取的需要的数据,直接代入到网络中即可求解
• 损失函数和激活函数: 我们BFDNN模型中选用的损失函数是交叉熵损失函数以及Relu和Sigmoid两个非线性激活函数改进DNN算法收敛速度,之所以这样搭配是因为在用Sigmoid函数作为激活函数的时候，交叉熵损失函数比平方差损失函数的效果更加出色.
• 优化函数 - 使用Dropout层,这里我们使用dropout很好地防止了在训练过程中的过拟合现象.

以上暂时为本人对该论文的一些浅薄的认识,会有继续的更新.