晓萌希望将1到N的连续整数组成的集合划分成两个子集合,且保证每个集合的数字和是相等。例如,对于N=3,对应的集合{1,2,3}能被划分成{3} 和 {1,2}两个子集合.
这两个子集合中元素分别的和是相等的。
对于N=3,我们只有一种划分方法,而对于N=7时,我们将有4种划分的方案。
输入包括一行,仅一个整数,表示N的值(1≤N≤39)。
输出包括一行,仅一个整数,晓萌可以划分对应N的集合的方案的个数。当没发划分时,输出0。
样例输入
7
样例输出
4
这道题一开始看不懂,虽然看标题知道是动态规划的类型题,但是一点思路都没有,后来去找了几个博客看,然后大概知道了这道题的做法,这道题的思路自己感觉是这样:
1)大体思路:首先想到是通过已知来,一步步推出从dp[1]到dp[sum = n*(n+1)/2]的一个方法数(dp[i]表示总集合和为i的一个方法数),然后第sum除于2,这就是问题的答案了,但是如何求出dp[1]到dp[sum]的数?
2)可以通过二维的方法求dp[1~sum]的数:
1:如果这第i个元素本身大于子集合的整数和sum,即i>sum,那么这第i个元素肯定不能加入子集合,否则就超出子集合整数和限制了。此时:F(i, sum)=F(i-1, sum),意思就是在相等的子集合整数和限制下,既然第i个元素没被加入,那么判断完第i个元素后的整数选取方案与判断完第i-1个数时的方案应该是相同的。
2:如果这第i个元素小于子集合整数和,那么就有两种考虑:
2.1:坚持不把第i个元素放入子集合,那么此时整数的选取方案仍然有F(i-1, sum)种。
2.2:如果把第i个元素放入了子集合,那么此时整数的选取方案有F(i-1, sum-i)种,sum-i的含义在于既然要放入第i个元素,就要给它留下足够的空间。F(i-1, sum-i)是在肯定要放入元素i的情形下,放入元素i前,整数的选取方案。
也即是说,i<=sum时,F(i, sum)=F(i-1, sum)+F(i-1, sum-i)。
综上可得:
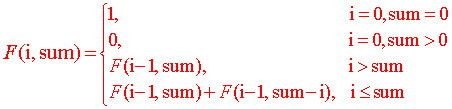
代码如下:
#include<iostream>
using namespace std;
long long DP[50][5000];
int main(){
int n;
cin>>n;
int s=(1+n)*n/2;
if(s&1) {
cout<<0;return 0;}//这个是判断是否能够分成两组,因为每一组的值都是总和的一半,所以总和必须是偶数。
int ss = s/2;
DP[0][0]=1;//这个就是关键的初值:当我背包的重量为0时,考虑前0个数,也就是把0放到包里这一种情况,所以情况数为1.
for(int i=1;i<=ss;i++){
DP[0][i] = 0;//当我背包容量为i时(i>0),这个时候在前0个数中无法找到任何组能满足我的这个需求,所以为0.
}
for(int i=1;i<=n;i++){
for(int h=0;h<=ss;h++){
if(h<i) DP[i][h]=DP[i-1][h];//当h<i时,意味着背包需求为h,但是我i已经大于h了,意味着肯定不能把i放进背包,所以当前情况为上一种情况。
else{
DP[i][h]=DP[i-1][h]+DP[i-1][h-i];//这就是那个动态方程(上面内容已经讲了)
//cout <<DP[i][h] << endl;
}
// cout << DP[i][h] << ' ';
}
//cout << endl;
}
cout<<DP[n][ss]/2<<endl;//输出的时候要/2。因为我的里面分成了两组,得出的结果是有一半其实属于同一个情况的
}