目录
PERFORMANCE ANALYSIS FOR LOCALIZATION ALGORITHMS
CRLB给出了使用相同数据的任何无偏估计可获得的方差的下界,因此它可以作为与定位算法的均方误差(MSE)进行比较的重要基准。 然而,有偏估计的MSE可能小于CRLB。
在第1节中提供了在存在高斯噪声的情况下使用TOA测量进行CRLB计算的过程。 在第2节中,我们给出了定位估计量的理论均值和MSE表达式,其推导基于成本函数的最小化或最大化。
1 CRLB Computation
生成CRLB的关键是构造相应的Fisher信息矩阵(FIM)。 FIM逆的对角元素是可实现的最小方差值。 考虑公式2.1的一般测量模型,使用以下步骤总结计算CRLB的标准程序:


或者,当测量误差为零 - 均值高斯分布时,I(x)也可以计算为[20]
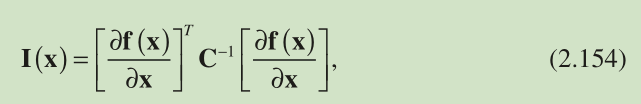
where C denotes the covariance matrix for n . We now utilize Equation 2.154 to determine the FIMs for positioning with TOA measure -ments based on Equations 2.8 and their associated noise covariance matrices, respectively. The FIM based on TOA measurements of Equation 2.5 , denoted by , is

注:


It is straightforward to show that

Employing Equations 2.156 and 2.11 , Equation 2.155 becomes
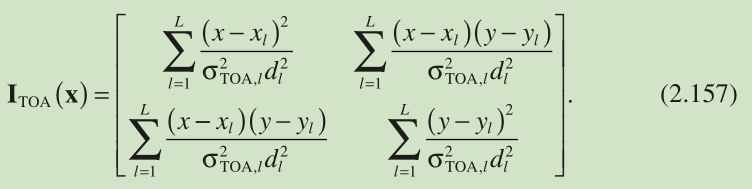
注:
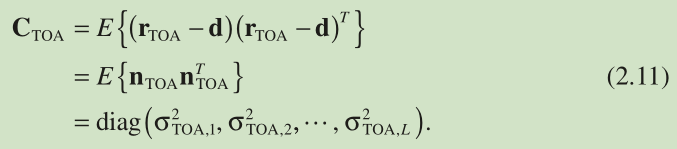

2 Mean and Variance Analysis
When the position estimator corresponds to minimizing or maximizing a continuous cost function, the mean and MSE expressions of can be produced with the use of Taylor ’ s series expansion as follows [25] . Let
be a general continuous function of
and the estimate
is given by its minimum or maximum. This implies that
当位置估计器对应于最小化或最大化连续成本函数时, 的均值和MSE表达式可以使用泰勒级数展开产生如下[25]。 设
是
的一般连续函数,估计
由其最小值或最大值给出。 这意味着

At small estimation error conditions, such that is located at a reasonable proximity of the ideal solution of x , using Taylor ’ s series to expand Equation 2.165 around x up to the first - order terms, we have
在小的估计误差条件下,使得 位于x 的理想解的合理接近处,使用泰勒级数将公式2.165扩展到 x 到一阶项,我们有

where and
are the corresponding Hessian matrix and gradient vector evaluated at the true location. When the second- order derivatives inside the Hessian matrix are smooth enough around x , we have [29] :
其中和
是在真实位置评估的相应Hessian矩阵和梯度向量。 当Hessian矩阵内的二阶导数在 x 周围足够平滑时,我们有[29]:

Employing Equation 2.167 and taking the expected value of Equation 2.166 yield the mean of :
采用公式2.167并取公式2.166的预期值得出平均值:

When is an unbiased estimate of x ,
indicating that the last term in Equation 2.168 is a zero vector.
式子2.168的后半部分是零向量。由于Hessian的逆不为零,那么梯度向量为零。
Utilizing Equations 2.166 and 2.167 again and the symmetric property of the Hessian matrix, we obtain the covariance for denoted by
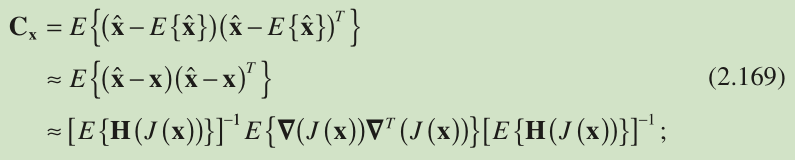
that is, the variances of the estimates of x and y are given by and
, respectively.
对角线上的数是x,y的方差。
下面是具体的实例,以ML为例:
We first take the ML cost function for TOA-based positioning in Equation 2.59 , namely, , as an illustration. As
, the expected value of
can be easily determined with the use of Equations 2.61 – 2.64 as
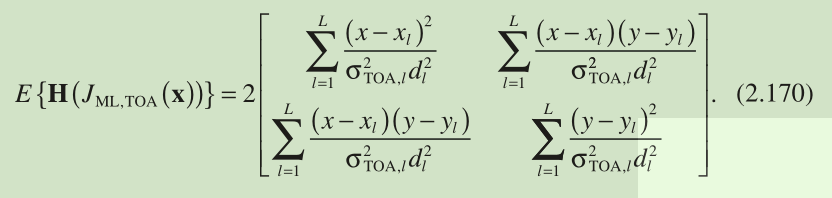
注:
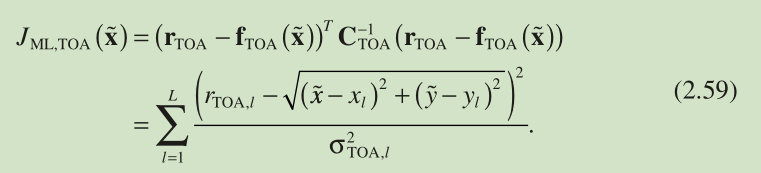


On the other hand, the expected value of is
![]()

注:

这意味着ML估计在其方差达到公式2.158中的CRLB的意义上是最优的。
均值和方差表达式也可以应用于线性方法,其对应于二次成本函数的最小化。 考虑公式2.119中的WLLS成本函数,相应的Hessian矩阵和梯度向量确定为


总体看来,挺困难的一些公式