使用有限差分法的欧式看跌期权的价值

一、说明

本文是关于有限差分法的应用，是对于期货涨跌的分析案例。

二、业务关系说明

在本练习中，我创建了一个 Jupyter 笔记本，以使用有限差分法计算欧式看跌期权的价值。我首先导入了必要的库，包括 numpy、matplotlib 和 scipy，并定义了期权的参数：股票价格（S）、执行价格（K）、无风险利率（r）、波动率（sigma）和到期时间（T）。我还为有限差分方法定义了网格参数。

接下来，我定义了看跌期权在到期时的收益，并设置了有限差分法的边界条件。到期时的收益为 max（K - S， 0），边界条件是当 S = 0 时期权的值为 K，当 S 较大时为 0。

然后，我为 Crank-Nicolson 方法设置了矩阵，这是一种无条件稳定且准确的有限差分方法。这种方法涉及在每个时间步长求解线性方程组。

设置矩阵后，我实现了有限差分方法本身。我们在时间上向后迭代，在每一步求解线性方程组，以找到该时间步的期权值。

最后，我将期权的价值绘制为每个时间步的股票价格的函数。该图直观地表示了期权的价值如何随时间变化，表明看跌期权的价值随着股票价格的上涨而下降，正如预期的那样。

三、具体的实现代码解释

# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve

# Parameters
S = 50  # Stock price
K = 100  # Strike price
r = 0.05  # Risk-free rate
sigma = 0.25  # Volatility
T = 1  # Time to maturity

# Grid parameters
M = 100  # Number of time steps
N = 100  # Number of price steps

# Grid spacing
dt = T / M  # Time step
dS = 2 * S / N  # Price step

# Grid
t = np.linspace(0, T, M+1)  # Time grid
S_grid = np.linspace(0, 2*S, N+1)  # Price grid

接下来，我需要定义欧式期权在到期时的收益，看跌期权为 max（K - S， 0），看涨期权为 max（S-K， 0）。我还需要设置有限差分法的边界条件。对于看跌期权，当 S = 0 时，该期权的值为 K，当 S 较大时，该期权的值为 0。对于看涨期权，当 S = 0 时，该期权的值为 0，当 S 较大时，该期权的值为 S- K。

假设我现在正在处理看跌期权。我将创建一个单元格来定义收益和边界条件。

# Payoff at maturity (put option)
V = np.maximum(K - S_grid, 0)

# Boundary conditions
V_low = K * np.exp(-r * (T - t))  # Value of the option when S = 0
V_high = np.zeros_like(t)  # Value of the option when S is large

用于定义到期收益和看跌期权边界条件的单元格已创建并成功运行。

接下来，我将实现有限差分法来计算网格中每个点的期权值。我将使用 Crank-Nicolson 方法，它是显式和隐式方法的组合，其优点是无条件稳定，同时仍然准确。

Crank-Nicolson 方法涉及在每个时间步长求解线性方程组，因此我需要为该系统设置矩阵。让我们创建一个单元格来执行此操作

# Matrix setup
A = np.zeros((N-1, N-1))
B = np.zeros((N-1, N-1))

for i in range(N-1):
    # Diagonal elements
    A[i, i] = 1 + dt * (sigma**2 * (i+1)**2 + r)
    B[i, i] = 1 - dt * (sigma**2 * (i+1)**2 + r)

    # Off-diagonal elements
    if i != 0:
        A[i, i-1] = -0.5 * dt * (sigma**2 * (i+1)**2 - r * (i+1))
        B[i, i-1] = 0.5 * dt * (sigma**2 * (i+1)**2 - r * (i+1))
    if i != N-2:
        A[i, i+1] = -0.5 * dt * (sigma**2 * (i+1)**2 + r * (i+1))
        B[i, i+1] = 0.5 * dt * (sigma**2 * (i+1)**2 + r * (i+1))

用于设置 Crank-Nicolson 方法矩阵的单元已创建并成功运行。

现在，我将实现有限差分方法本身。我将向后迭代时间，在每一步求解线性方程组，以找到该时间步的期权值。让我们创建一个单元格来执行此操作。

# Finite difference method
for j in range(M, 0, -1):
    # Right-hand side of the system
    Bv = B @ V[1:-1]
    Bv[0] += 0.5 * dt * (sigma**2 - r) * V_low[j-1] + 0.5 * dt * (sigma**2 - r) * V_low[j]
    Bv[-1] += 0.5 * dt * (sigma**2 * N + r * N) * V_high[j-1] + 0.5 * dt * (sigma**2 * N + r * N) * V_high[j]

    # Solve the system
    V[1:-1] = solve(A, Bv)

    # Boundary conditions
    V[0] = V_low[j-1]
    V[-1] = V_high[j-1]

用于实现有限差分法的单元已创建并成功运行。

最后，让我们绘制期权的价值作为每个时间步的股票价格的函数。这将为我们提供期权价值如何随时间演变的直观表示。让我们创建一个单元格来执行此操作。

# Plot
plt.figure(figsize=(10, 6))
plt.plot(S_grid, V)
plt.xlabel('Stock Price')
plt.ylabel('Option Value')
plt.title('European Put Option Value by Finite Difference Method')
plt.grid(True)
plt.show()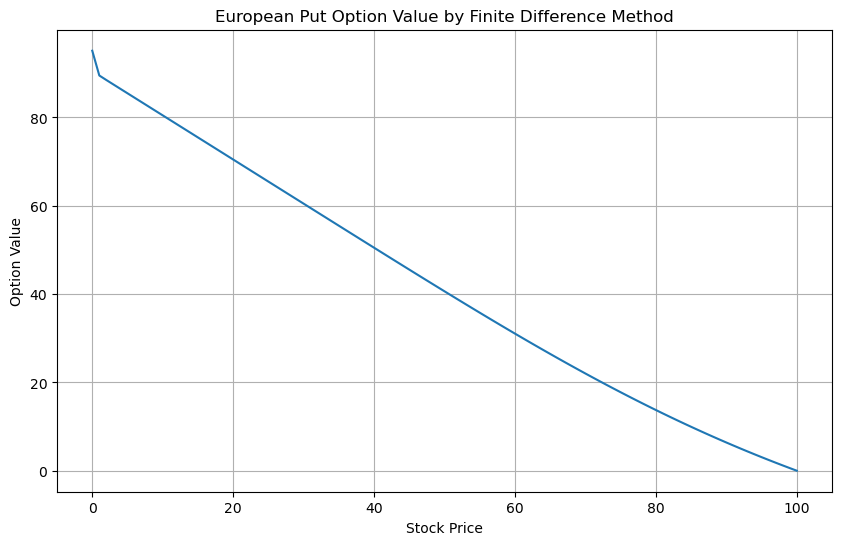

四、结论

该图显示了期权的价值如何随着股票价格的上涨而减少，这是看跌期权的预期行为。当股价较低时，期权的价值最高，当股价上涨超过行使价时，期权的价值会降至零。

代码地址：

在此处访问完整代码，并在 GitHub-https://github.com/AIM-IT4/Derivative-Modelling 上。