2.2 偏微分方程的差分解法
2.2.1 二维泊松方程
考虑区域 Ω \Omega Ω 上的二维泊松问题:
{ − ( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 ) u = f ( x , y ) , ( x , y ) ∈ Ω u ∣ ∂ Ω = φ ( x , y ) , (2-16) \left\{\begin{array}{l} -\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) u=f(x, y), \quad(x, y) \in \Omega \\ \left.u\right|_{\partial \Omega}=\varphi(x, y), \end{array}\right.\tag{2-16} {
−(∂x2∂2+∂y2∂2)u=f(x,y),(x,y)∈Ωu∣∂Ω=φ(x,y),(2-16)
其中, ∂ Ω \partial \Omega ∂Ω 为区域 Ω \Omega Ω 的边界, f ( x , y ) f(x, y) f(x,y) 和 φ ( x , y ) \varphi(x, y) φ(x,y) 为已知函数。 u ∣ ∂ Ω = φ ( x , y ) u\mid_{\partial \Omega}=\varphi(x, y) u∣∂Ω=φ(x,y) 描述了函数 u u u 在 边界上的取值, 即所谓的边界条件。为简单起见, 这里仅讨论 Ω \Omega Ω 为矩形的情况, 即 a < x < b a<x<b a<x<b, c < y < d c<y<d c<y<d 。首先, 用间隔 h 1 = ( b − a ) / N 、 h 2 = ( d − c ) / M h_1=(b-a) / N 、 h_2=(d-c) / M h1=(b−a)/N、h2=(d−c)/M 分别将 x x x 轴上的区间 [ a , b ] 、 y [a, b] 、 y [a,b]、y 轴上的区间 [ c , d ] [c, d] [c,d] 划分为 N 、 M N 、 M N、M 等分, 得 x i = a + i h 1 、 0 ⩽ i ⩽ N x_i=a+i h_1 、 0 \leqslant i \leqslant N xi=a+ih1、0⩽i⩽N 和 y j = c + j h 2 、 0 ⩽ j ⩽ M y_j=c+j h_2 、 0 \leqslant j \leqslant M yj=c+jh2、0⩽j⩽M 。再根据 x i x_i xi 和 y j y_j yj 对矩形 区域进行网格剖分, 如下图所示。横线与坚线的交点就是网格结点, 称位于边界 ∂ Ω \partial \Omega ∂Ω 上的 结点为边界结点, 其余结点为内结点。

在内结点处考虑泊松问题:
− [ ∂ 2 u ( x i , y j ) ∂ x 2 + ∂ 2 u ( x i , y j ) ∂ y 2 ] = f ( x i , y j ) , 1 ⩽ i ⩽ N − 1 , 1 ⩽ j ⩽ M − 1 (2-17) -\left[\frac{\partial^2 u\left(x_i, y_j\right)}{\partial x^2}+\frac{\partial^2 u\left(x_i, y_j\right)}{\partial y^2}\right]=f\left(x_i, y_j\right), \quad 1 \leqslant i \leqslant N-1, \quad 1 \leqslant j \leqslant M-1\tag{2-17} −[∂x2∂2u(xi,yj)+∂y2∂2u(xi,yj)]=f(xi,yj),1⩽i⩽N−1,1⩽j⩽M−1(2-17)
由泰勒公式, 有:
∂ 2 u ( x i , y j ) ∂ x 2 = 1 h 1 2 [ u ( x i − 1 , y j ) − 2 u ( x i , y j ) + u ( x i + 1 , y j ) ] − h 1 2 12 ∂ 4 u ( ξ i j , y j ) ∂ x 4 , x i − 1 < ξ i j < x i + 1 (2-18) \begin{gathered} \frac{\partial^2 u\left(x_i, y_j\right)}{\partial x^2}=\frac{1}{h_1^2}\left[u\left(x_{i-1}, y_j\right)-2 u\left(x_i, y_j\right)+u\left(x_{i+1}, y_j\right)\right]-\frac{h_1^2}{12} \frac{\partial^4 u\left(\xi_{i j}, y_j\right)}{\partial x^4}, \\ x_{i-1}<\xi_{i j}<x_{i+1} \end{gathered}\tag{2-18} ∂x2∂2u(xi,yj)=h121[u(xi−1,yj)−2u(xi,yj)+u(xi+1,yj)]−12h12∂x4∂4u(ξij,yj),xi−1<ξij<xi+1(2-18)
∂ 2 u ( x i , y j ) ∂ y 2 = 1 h 2 2 [ u ( x i , y j − 1 ) − 2 u ( x i , y j ) + u ( x i , y j + 1 ) ] − h 2 2 12 ∂ 4 u ( x i , η i j ) ∂ y 4 , y j − 1 < η i j < y j + 1 (2-19) \begin{gathered} \frac{\partial^2 u\left(x_i, y_j\right)}{\partial y^2}=\frac{1}{h_2^2}\left[u\left(x_i, y_{j-1}\right)-2 u\left(x_i, y_j\right)+u\left(x_i, y_{j+1}\right)\right]-\frac{h_2^2}{12} \frac{\partial^4 u\left(x_i, \eta_{i j}\right)}{\partial y^4}, \\ y_{j-1}<\eta_{i j}<y_{j+1} \end{gathered}\tag{2-19} ∂y2∂2u(xi,yj)=h221[u(xi,yj−1)−2u(xi,yj)+u(xi,yj+1)]−12h22∂y4∂4u(xi,ηij),yj−1<ηij<yj+1(2-19)
将以上两式代入式 ( 2 − 17 ) (2-17) (2−17), 忽略小量 O ( h 1 2 + h 2 2 ) O\left(h_1{ }^2+h_2{ }^2\right) O(h12+h22), 并使用简写 u i j = u ( x i , y j ) u_{i j}=u\left(x_i, y_j\right) uij=u(xi,yj), 得到差分 格式 (2-20)。所谓差分格式, 就是用几个相邻数值点的差商来替代方程中的导数或偏导数 的近似算法。
− 1 h 2 2 u i , j − 1 − 1 h 1 2 u i − 1 , j + 2 ( 1 h 1 2 + 1 h 2 2 ) u i , j − 1 h 1 2 u i + 1 , j − 1 h 2 2 u i , j + 1 = f ( x i , y j ) , 1 ⩽ i ⩽ N − 1 , 1 ⩽ j ⩽ M − 1 (2-20) \begin{gathered} -\frac{1}{h_2^2} u_{i, j-1}-\frac{1}{h_1^2} u_{i-1, j}+2\left(\frac{1}{h_1^2}+\frac{1}{h_2^2}\right) u_{i, j}-\frac{1}{h_1^2} u_{i+1, j}-\frac{1}{h_2^2} u_{i, j+1}=f\left(x_i, y_j\right), \\ 1 \leqslant i \leqslant N-1, \quad 1 \leqslant j \leqslant M-1 \end{gathered}\tag{2-20} −h221ui,j−1−h121ui−1,j+2(h121+h221)ui,j−h121ui+1,j−h221ui,j+1=f(xi,yj),1⩽i⩽N−1,1⩽j⩽M−1(2-20)
先定义向量 u j : \boldsymbol{u}_j: uj:
u j = ( u 1 j , u 2 j , … , u N − 1 , j ) T , 0 ⩽ j ⩽ M (2-21) \boldsymbol{u}_j=\left(u_{1 j}, \quad u_{2 j}, \quad \ldots, \quad u_{N-1, j}\right)^{\mathrm{T}}, \quad 0 \leqslant j \leqslant M\tag{2-21} uj=(u1j,u2j,…,uN−1,j)T,0⩽j⩽M(2-21)
再将差分格式 (2-20) 写为矩阵形式:
D u j − 1 + C u j + D u j + 1 = f j , 1 ⩽ j ⩽ M − 1 (2-22) \boldsymbol{D} \boldsymbol{u}_{j-1}+\boldsymbol{C} \boldsymbol{u}_j+\boldsymbol{D} \boldsymbol{u}_{j+1}=\boldsymbol{f}_j, \quad 1 \leqslant j \leqslant M-1\tag{2-22} Duj−1+Cuj+Duj+1=fj,1⩽j⩽M−1(2-22)
其中, 矩阵 C 、 D 、 \boldsymbol{C} 、 \boldsymbol{D} 、 C、D、 向量 f j \boldsymbol{f}_j fj 的定义如下, 注意向量 f j \boldsymbol{f}_j fj 的首尾元素已包含了 x = a x=a x=a 和 x = b x=b x=b 处的边界条件。
C = ( 2 ( 1 h 1 2 + 1 h 2 2 ) − 1 h 1 2 − 1 h 1 2 2 ( 1 h 1 2 + 1 h 2 2 ) − 1 h 1 2 ⋱ ⋱ ⋱ − 1 h 1 2 2 ( 1 h 1 2 + 1 h 2 2 ) − 1 h 1 2 − 1 h 1 2 2 ( 1 h 1 2 + 1 h 2 2 ) ) (2-23) \boldsymbol{C}=\left(\begin{array}{ccccc} 2\left(\frac{1}{h_1^2}+\frac{1}{h_2^2}\right) &-\frac{1}{h_1^2} & & & \\ -\frac{1}{h_1^2} & 2\left(\frac{1}{h_1^2}+\frac{1}{h_2^2}\right) & -\frac{1}{h_1^2} & & \\ & \ddots & \ddots & \ddots & \\ & & -\frac{1}{h_1^2} & 2\left(\frac{1}{h_1^2}+\frac{1}{h_2^2}\right) & -\frac{1}{h_1^2} \\ & & & -\frac{1}{h_1^2} & 2\left(\frac{1}{h_1^2}+\frac{1}{h_2^2}\right) \end{array}\right)\tag{2-23} C=
2(h121+h221)−h121−h1212(h121+h221)⋱−h121⋱−h121⋱2(h121+h221)−h121−h1212(h121+h221)
(2-23)
D = ( − 1 h 2 2 − 1 h 2 2 ⋱ − 1 h 2 2 − 1 h 2 2 ) , f j = ( f ( x 1 , y j ) + 1 h 1 2 φ ( x 0 , y j ) f ( x 2 , y j ) ⋮ f ( x N − 2 , y j ) f ( x N − 1 , y j ) + 1 h 1 2 φ ( x N , y j ) ) (2-24) \boldsymbol{D}=\left(\begin{array}{cccc} -\frac{1}{h_2^2} & & & \\ & -\frac{1}{h_2^2} & & \\ & & \ddots & \\ & & -\frac{1}{h_2^2} & \\ & & & -\frac{1}{h_2^2} \end{array}\right), \boldsymbol{f}_j=\left(\begin{array}{c} f\left(x_1, y_j\right)+\frac{1}{h_1^2} \varphi\left(x_0, y_j\right) \\ f\left(x_2, y_j\right) \\ \vdots \\ f\left(x_{N-2}, y_j\right) \\ f\left(x_{N-1}, y_j\right)+\frac{1}{h_1^2} \varphi\left(x_N, y_j\right) \end{array}\right)\tag{2-24} D=
−h221−h221⋱−h221−h221
,fj=
f(x1,yj)+h121φ(x0,yj)f(x2,yj)⋮f(xN−2,yj)f(xN−1,yj)+h121φ(xN,yj)
(2-24)
式 (2-22) 还可以进一步写成如下的矩阵形式, 注意等号右边向量的首尾元素加入了 y = c y=c y=c 和 y = d y=d y=d 处的边界条件。
( C D D C D ⋱ ⋱ ⋱ D C D D C ) ( u 1 u 2 ⋮ u M − 2 u M − 1 ) = ( f 1 − D u 0 f 2 ⋮ f M − 2 f M − 1 − D u M ) (2-25) \left(\begin{array}{ccccc} C & D & & & \\ D & C & D & & \\ & \ddots & \ddots & \ddots & \\ & & D & C & D \\ & & & D & C \end{array}\right)\left(\begin{array}{c} \boldsymbol{u}_1 \\ \boldsymbol{u}_2 \\ \vdots \\ \boldsymbol{u}_{M-2} \\ \boldsymbol{u}_{M-1} \end{array}\right)=\left(\begin{array}{c} \boldsymbol{f}_1-\boldsymbol{D} \boldsymbol{u}_0 \\ \boldsymbol{f}_2 \\ \vdots \\ \boldsymbol{f}_{M-2} \\ \boldsymbol{f}_{M-1}-\boldsymbol{D} \boldsymbol{u}_M \end{array}\right)\tag{2-25}
CDDC⋱D⋱D⋱CDDC
u1u2⋮uM−2uM−1
=
f1−Du0f2⋮fM−2fM−1−DuM
(2-25)
因此, 矩形 Ω \Omega Ω 上的二维泊松问题就转化为上面形如 A u = f \boldsymbol{A} \boldsymbol{u}=\boldsymbol{f} Au=f 的矩阵问题。对于这类问题, 最直接的解法就是先求 A \boldsymbol{A} A 的逆矩阵 A − 1 \boldsymbol{A}^{-1} A−1, 然后 u = A − 1 f \boldsymbol{u}=\boldsymbol{A}^{-1} \boldsymbol{f} u=A−1f 即可, 这在 Matlab 中可用左除 \ 实现。注意式 (2-22)只针对内结点, 所以 C 、 D \boldsymbol{C} 、 \boldsymbol{D} C、D 均是 N − 1 N-1 N−1 阶方阵, A \boldsymbol{A} A 是 ( N − 1 ) ( M − 1 ) (N-1)(M-1) (N−1)(M−1) 阶方 阵。下面给出一个实际例子。
{ − ( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 ) u = ( π 2 − 1 ) e x sin ( π y ) , 0 < x < 2 , 0 < y < 1 u ( 0 , y ) = sin ( π y ) , u ( 2 , y ) = e 2 sin ( π y ) , 0 ⩽ y ⩽ 1 u ( x , 0 ) = 0 , u ( x , 1 ) = 0 , 0 < x < 2 (2-26) \left\{\begin{array}{lll} -\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) u=\left(\pi^2-1\right) \mathrm{e}^x \sin (\pi y), & 0<x<2, & 0<y<1 \\ u(0, y)=\sin (\pi y), & u(2, y)=\mathrm{e}^2 \sin (\pi y), & 0 \leqslant y \leqslant 1 \\ u(x, 0)=0, & u(x, 1)=0, & 0<x<2 \end{array}\right.\tag{2-26} ⎩
⎨
⎧−(∂x2∂2+∂y2∂2)u=(π2−1)exsin(πy),u(0,y)=sin(πy),u(x,0)=0,0<x<2,u(2,y)=e2sin(πy),u(x,1)=0,0<y<10⩽y⩽10<x<2(2-26)
根据式 (2-25) 求解这个泊松问题, 代码如下:
主程序代码如下
clear; close all;
%生成网格上的坐标
h=0.1; x=[0:h:2]'; y=[0:h:1]';
N=length(x)-1; M=length(y)-1;
[X,Y]=meshgrid(x,y);
%解析解
u_analytical=exp(X).*sin(pi*Y);
X=X(2:M,2:N); Y=Y(2:M,2:N);
%生成f(x,y)的矩阵
f=(pi^2-1)*exp(X).*sin(pi*Y);
f(:,1)=f(:,1)+sin(pi*y(2:M))/h^2;
f(:,end)=f(:,end)+exp(2)*sin(pi*y(2:M))/h^2;
%构造矩阵D、C、A
e=ones(N-1,1);
C=1/h^2*spdiags([-e 4*e -e],[-1 0 1],N-1,N-1);
D=-1/h^2*eye(N-1);
e=ones(M-1,1);
A=kron(eye(M-1),C)+kron(spdiags([e e],[-1 1],M-1,M-1),D);
%左除求解
f=f'; u=zeros(M+1,N+1);
u(2:M,2:N)=reshape(A\f(:),N-1,M-1)';
u(:,1)=sin(pi*y); u(:,end)=exp(2)*sin(pi*y);
%画图
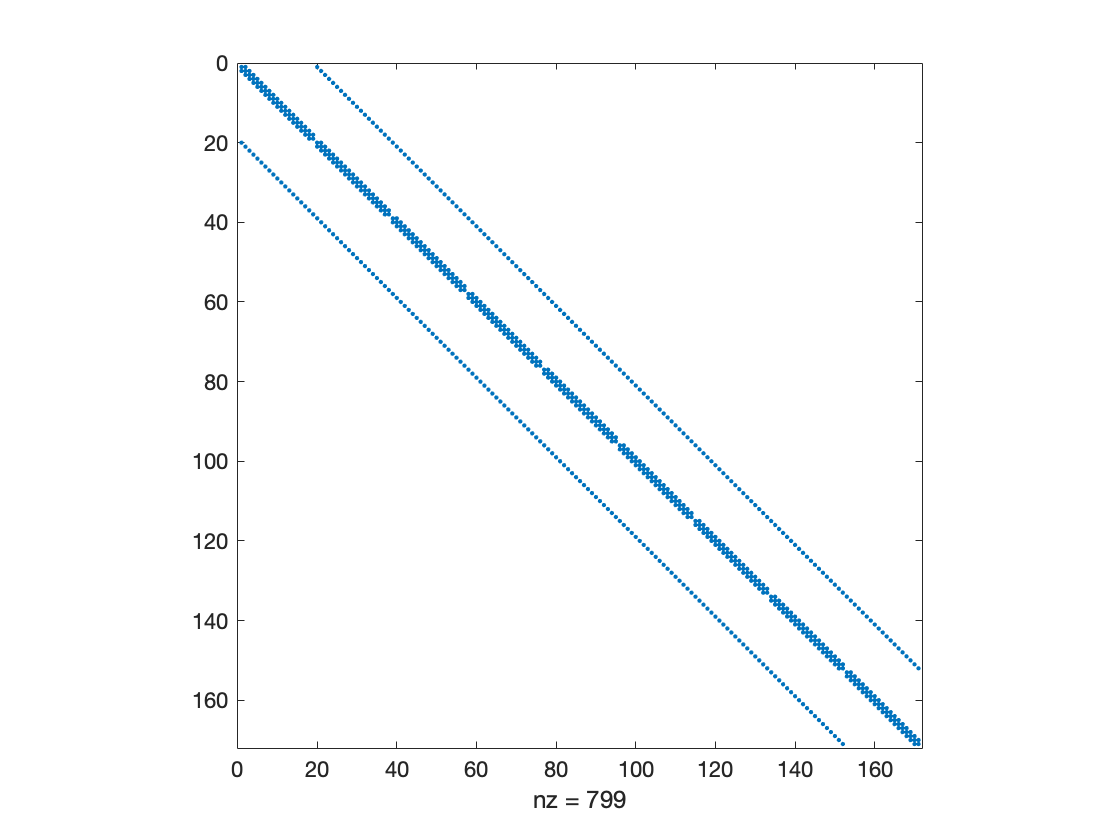
figure(1), spy(A,5)
figure(2), subplot(2,2,1), mesh(x,y,u)
xlabel x, ylabel y, zlabel u
subplot(2,2,2), mesh(x,y,u-u_analytical)
axis([0 2 0 1 0 0.04])
xlabel x, ylabel y, zlabel Error
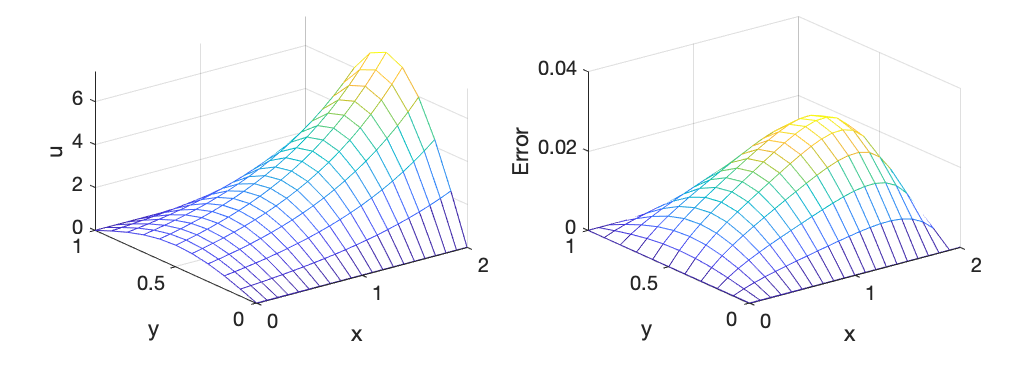
程序输出结果如图所示, 左图为 h 1 = h 2 = 0.1 h_1=h_2=0.1 h1=h2=0.1 时泊松问题 (2-26) 的数值解, 右图为数值解与解析解 u = e x sin ( π y ) u=\mathrm{e}^x \sin (\pi y) u=exsin(πy) 之间的误差。当然, 进一步缩小 h 1 h_1 h1 和 h 2 h_2 h2 会以增加运算量为代价降低这个误差。
为了使读者产生直观的理解, 下图显示了 h 1 = h 2 = 0.2 h_1=h_2=0.2 h1=h2=0.2 时方阵 A \boldsymbol{A} A 的非零元素分布情况。